Formule de Toricelli
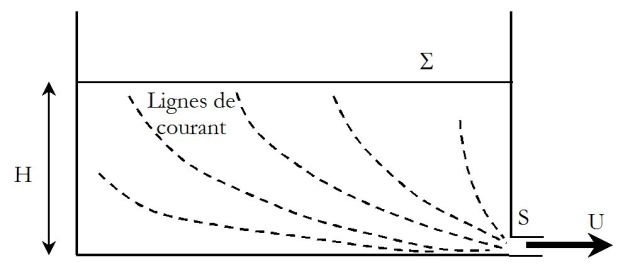
En étudiant l'écoulement de l'eau par un orifice de surface S percé dans le bas d'une cuve, Torricelli observa que le jet sortait perpendiculairement à la surface S, avec un débit volumique
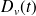proportionnel à S et à la racine carrée de la hauteur d'eau
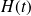dans la cuve.
Comment interpréter ce résultat ?
La conservation du débit volumique donne :
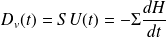
Où
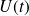est la vitesse de sortie dans le jet et
la section de la cuve.
Comme
, on en déduit que :
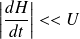
On peut se placer en régime quasi-stationnaire en supposant
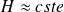et utiliser la relation de Bernoulli en régime stationnaire.
On se place sur une ligne de courant (voir figure).
Le jet d'eau étant à l'air libre, sa pression est celle du gaz qui l'entoure, c'est-à-dire la pression atmosphérique
.
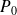Il en est de même pour la surface libre dans la cuve.
Le théorème de Bernoulli donne alors :
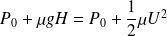
Par conséquent :
On obtient une loi analogue à la loi de la chute libre dans le champ de pesanteur : c'est la formule de Torricelli.
Ensuite, le jet suit une loi de chute libre avec la vitesse initiale U horizontale, d'où la forme parabolique du jet.
Attention : Vidange d'un réservoir dans l'ARQS (formule de Torricelli.)
Complément : Quand peut-on se placer dans l'ARQS ?
On compare l'accélération locale et l'accélération convective :
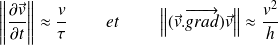
Où
est un ordre de grandeur du champ des vitesses et
la durée caractéristique de variation temporelle de ce champ.
La conservation du débit volumique entre la surface libre et le trou donne :
D'où :
Ainsi, si la section de sortie est bien négligeable devant la surface plane du liquide, l'accélération locale sera bien négligeable devant l'accélération convective. On pourra ainsi se placer dans l'ARQS et écrire que :
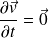
Exemple : Temps de vidange d'un réservoir
Le liquide considéré est un fluide parfait en écoulement incompressible.
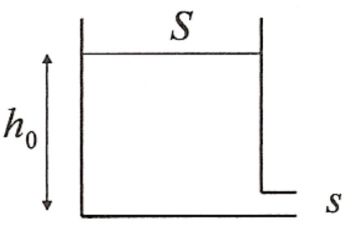
On suppose que
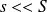: on peut ainsi se placer dans l'ARQS.
Soit
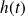la hauteur d'eau à l'instant
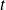, la formule de Torricelli donne la vitesse de l'écoulement en sortie :
La conservation du débit volumique donne :
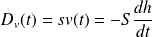
On obtient ainsi une équation différentielle vérifiée par
:
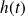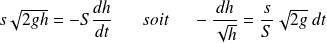
Par intégration :
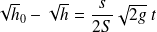
La durée de vidange
s'obtient en écrivant que
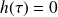, soit :
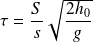
Simulation : Animation JAVA de JJ.Rousseau (Université du Mans)
Écoulement d'un liquide : cliquer ICI
