Pour tester sa connaissance du cours
Question
Soit un fluide newtonien de viscosité dynamique η, en écoulement avec un champ de vitesses du type
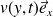 . Donner l'expression de la contrainte tangentielle exercée par le fluide situé au dessous de la cote y sur le fluide situé au dessus de cette cote y.
. Donner l'expression de la contrainte tangentielle exercée par le fluide situé au dessous de la cote y sur le fluide situé au dessus de cette cote y.Quelle est l'expression volumique des forces de viscosité s'exerçant sur un fluide visqueux incompressible et newtonien ?
Pour un écoulement unidirectionnel, tel que
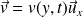 , la force de surface tangentielle , appelée force de cisaillement ou de viscosité, qui s'exerce à travers une surface d'aire S normale à vaut (il s'agit de la force exercée par la couche supérieure sur la couche inférieure) :
, la force de surface tangentielle , appelée force de cisaillement ou de viscosité, qui s'exerce à travers une surface d'aire S normale à vaut (il s'agit de la force exercée par la couche supérieure sur la couche inférieure) : 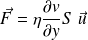
La viscosité a pour effet, dans un écoulement unidirectionnel, d'accélérer les éléments lents et de freiner les éléments rapides. Il s'agit donc d'un transfert interne de quantité de mouvement, qui présente les caractéristiques d'une diffusion de quantité de mouvement.
La force volumique de viscosité est :

Question
Donner la définition du débit volumique
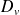 et du débit massique
et du débit massique
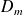 et d'un fluide en écoulement. Quelle est la relation entre les deux ?
et d'un fluide en écoulement. Quelle est la relation entre les deux ?
Débit volumique :
On appelle débit volumique
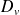 à travers une surface (S) orientée, le volume de fluide qui traverse (S) par unité de temps, compté positivement dans le sens du vecteur normal à la surface et négativement dans le cas contraire.
à travers une surface (S) orientée, le volume de fluide qui traverse (S) par unité de temps, compté positivement dans le sens du vecteur normal à la surface et négativement dans le cas contraire.Ce débit vaut :
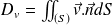
Débit massique :
Le débit massique
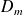 correspond à la masse de fluide qui traverse (S) par unité de temps, compté positivement dans le sens du vecteur normal à la surface et négativement dans le cas contraire :
correspond à la masse de fluide qui traverse (S) par unité de temps, compté positivement dans le sens du vecteur normal à la surface et négativement dans le cas contraire :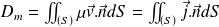
où
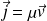 est le vecteur densité de courant ou vecteur densité de flux de masse de l'écoulement.
est le vecteur densité de courant ou vecteur densité de flux de masse de l'écoulement.Si le fluide est incompressible et homogène, donc si la masse volumique est constante et indépendante du point, alors :
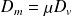
On peut remarquer que ces débits sont les équivalents de l'intensité électrique, du flux thermique et du débit de particules (vu en diffusion).
Question
Donner la définition puis l'expression du nombre de Reynolds. Quelle est sa dimension ?
Quelle est la relation entre le nombre de Reynolds
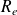 et l'épaisseur de la couche limite
et l'épaisseur de la couche limite
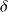 ?
?
Le nombre de Reynolds est défini comme étant l'ordre de grandeur du rapport du terme convectif sur le terme de diffusion :

où
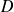 est une taille caractéristique de l'écoulement (la longueur de l'obstacle, par exemple) et
est une taille caractéristique de l'écoulement (la longueur de l'obstacle, par exemple) et
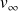 la vitesse du fluide loin de l'obstacle.
la vitesse du fluide loin de l'obstacle. L'épaisseur de la couche limite s'exprime en fonction du nombre de Reynolds :
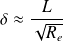
Question
Donner la définition du vecteur tourbillon d'un écoulement fluide.
Quelle est la définition d'un écoulement potentiel ?
Le vecteur tourbillon d'un écoulement fluide est :
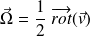
Un écoulement non tourbillonnaire est tel qu'en tout point de l'espace :

On peut alors définir (à une constante près) un potentiel des vitesses, noté
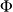 , par :
, par : 
L'écoulement est dit potentiel.
Question
Définir un écoulement incompressible.
Pour un écoulement potentiel, démontrer l'équation de Laplace.
Pour un écoulement incompressible :
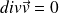
On en déduit que le débit volumique se conserve dans un tube de champ et donc concrètement dans une canalisation.
En particulier, si la vitesse est constante sur une section de la canalisation :
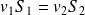
Ainsi, lorsque les lignes de champ d'un écoulement se resserrent, la norme du vecteur vitesse augmente.
Les relations
 et
et
 conduisent à l'équation de Laplace (vue également en électrostatique) :
conduisent à l'équation de Laplace (vue également en électrostatique) : 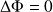
Question
Donner l'expression de l'accélération particulaire en fonction du champ eulérien des vitesses.
Question
Donner l'expression locale du principe de conservation de la masse.
C'est une équation de conservation classique :
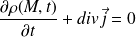
Question
Écrire l'équation d'Euler pour un écoulement parfait dans un référentiel galiléen.
Donner l'équation de Navier – Stokes pour un écoulement visqueux d'un fluide incompressible dans un référentiel galiléen.
Équation d'Euler pour un écoulement parfait dans un référentiel galiléen :

Ou encore :
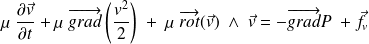
Équation de Navier – Stokes pour un écoulement visqueux d'un fluide incompressible dans un référentiel galiléen :
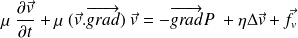
Question
Donner la relation de Bernoulli sur une ligne de courant dans un écoulement parfait, homogène, stationnaire et incompressible.
Donner la relation de Bernoulli au sein d'un écoulement parfait, homogène, stationnaire, incompressible et irrotationnel.
Sur une ligne de courant dans un écoulement parfait, homogène, stationnaire et incompressible :
Entre deux points A et B d'une même ligne de courant :

Au sein d'un écoulement parfait, homogène, stationnaire, incompressible et irrotationnel :
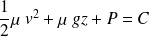
Question
De l'air (considéré comme un fluide parfait incompressible) est soufflé à travers une conduite dont la section change de
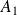 à
à
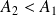 .
.
Un manomètre en U rempli de liquide a une branche connectée à la section
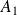 et l'autre branche à la section
et l'autre branche à la section
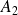 .
.
En considérant un rapport
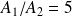 et une vitesse
et une vitesse
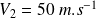 au niveau de la section
au niveau de la section
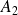 , calculer la différence de hauteur du liquide entre les deux branches du manomètre.
, calculer la différence de hauteur du liquide entre les deux branches du manomètre.
La masse volumique de l'air est
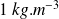 et celle du liquide dans le manomètre
et celle du liquide dans le manomètre
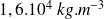 .
.
Question
Vidange d'un récipient : donner la formule de Torricelli. Quand s'applique-t-elle ?
La formule de Torricelli est :

 est la vitesse du fluide en sortie du trou et
est la vitesse du fluide en sortie du trou et
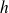 la hauteur de liquide au dessus du trou.
la hauteur de liquide au dessus du trou.
Cette formule s'applique rigoureusement quand la hauteur
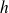 est constante. Elle s'applique également dans l'ARQS (
est constante. Elle s'applique également dans l'ARQS (
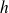 varie lentement avec le temps).
varie lentement avec le temps).
Question
Qu'appelle-t-on un écoulement de Poiseuille ?
Définir la résistance hydraulique.
Écoulement de Poiseuille :
Un fluide visqueux incompressible de densité
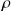 s'écoule dans un tube cylindrique de longueur L et de rayon R.
s'écoule dans un tube cylindrique de longueur L et de rayon R. La pression à l'entrée du tube (z = 0) est PE. La pression à la sortie du tube est PS.
La résistance hydraulique est :
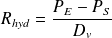
Où
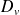 est le débit volumique de l'écoulement de Poisseuille.
est le débit volumique de l'écoulement de Poisseuille.
Question
On considère un fluide incompressible visqueux entre deux plans horizontaux parallèles séparés par une distance D=0,03 cm.
Le plan supérieur se déplace avec une vitesse constante
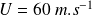 (écoulement de Couette).
(écoulement de Couette).
Considérant que le gradient de pression parallèle aux plans est nul et en considérant une viscosité
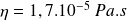 , déterminer la contrainte de cisaillement.
, déterminer la contrainte de cisaillement.






