Relation de Bernoulli
Cas d'un écoulement parfait, stationnaire, irrotationnel, incompressible et homogène
On suppose dans la suite que la seule force volumique (autre que les forces de pression) est le poids.
L'équation d'Euler devient :
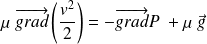
En notant : (l'axe (Oz) est orienté vers le haut)
Alors :
D'où :
Un champ scalaire dont le gradient est nul est indépendant du point M ; c'est une fonction du temps uniquement f(t).
Comme l'écoulement est stationnaire, cette fonction est constante :
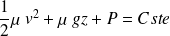
C'est le théorème de Bernoulli, qui affirme que la quantité
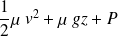reste en tout point du fluide égale à une même constante.
Remarque :
On remarque que
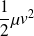et
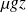désignent les énergies volumiques cinétique et potentielle (de pesanteur), homogènes à une pression.
Remarque :
Dans le cas particulier où
, on retrouve la relation fondamentale de l'hydrostatique des fluides :
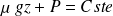
Attention : Relation de Bernoulli pour un écoulement parfait, stationnaire, irrotationnel, incompressible et homogène
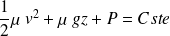
La constante est la même pour tous les points du fluide.
Cas d'un écoulement parfait, stationnaire, incompressible et homogène
On renonce à l'hypothèse « écoulement irrotationnel ». Alors :
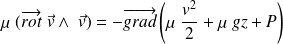
Afin d'éliminer le terme en rotationnel, on multiplie scalairement par
et on intègre le long d'une ligne de courant entre deux points A et B :
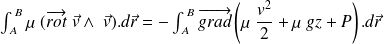
En tout point,
est parallèle au champ des vitesses : le terme
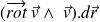est donc nul.
Ainsi :
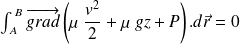
Soit :
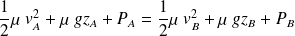
Ainsi, l'abandon de l'hypothèse « écoulement irrotationnel » restreint le théorème de Bernoulli aux points A et B d'une même ligne de courant.
Attention : Relation de Bernoulli pour un écoulement parfait, stationnaire, incompressible et homogène
L'abandon de l'hypothèse « écoulement irrotationnel » restreint le théorème de Bernoulli aux points A et B d'une même ligne de courant :
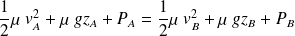
Cas d'un écoulement parfait, non stationnaire, irrotationnel, incompressible et homogène
L'équation d'Euler devient :
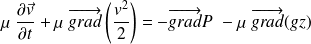
Soit :
Comme
, on peut définir un potentiel des vitesses tel que :
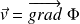
Alors, avec :
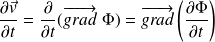
Il vient :
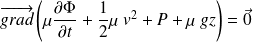
Soit une généralisation du théorème de Bernoulli dans le cas non stationnaire :
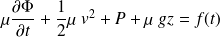
Où
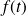est une fonction du temps uniquement.
Attention : Relation de Bernoulli pour un écoulement parfait, non stationnaire, irrotationnel, incompressible et homogène
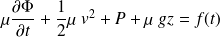
Où
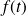est une fonction du temps uniquement et
est le potentiel des vitesses défini par :
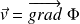
Remarque : Interprétation énergétique du théorème de Bernoulli
On se place dans le cas d'un écoulement parfait, stationnaire, irrotationnel, incompressible et homogène. Alors :
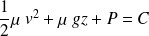
En multipliant par le volume
d'une particule de fluide :
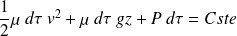
On reconnaît :
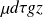: énergie potentielle de pesanteur de la particule de fluide.
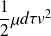: énergie cinétique de la particule de fluide.
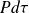: énergie potentielle associée aux forces de pression.
Le théorème de Bernoulli, plus général que la simple conservation de l'énergie mécanique d'un point matériel dans un milieu non continu, est un cas particulier du 1er principe :
Avec
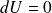et
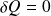: les hypothèses implicites de l'application du théorème de Bernoulli sont les aspects isothermes et adiabatiques de l'évolution.
En effet, pour un fluide parfait, l'énergie interne ne dépend que de la température.
Par ailleurs, l'aspect adiabatique de la transformation ne pose pas de problème particulier ; en l'absence de transfert thermique en provenance de l'extérieur du fluide, il n ‘y a pas de production de chaleur au sein même d'un fluide non visqueux.
Complément : Écoulement permanent et lent d'un fluide compressible
Peut-on appliquer le théorème de Bernoulli sous sa forme la plus simple à un fluide compressible comme l'air ?
On rappelle la définition du coefficient de compressibilité :
Il peut encore s'écrire en fonction de la masse volumique :
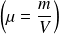
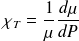
On suppose qu'il est possible de négliger les variations de
pour un écoulement permanent où la vitesse varie entre 0 et
.
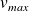D'après le théorème de Bernoulli (en l'absence de variation de la cote z), la pression varierait entre
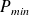et
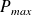avec :
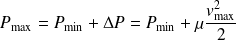
Une telle variation de pression est compatible avec l'hypothèse si la variation de
qui lui est liée est faible en valeur relative, soit si :
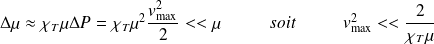
Or :
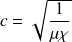
Correspond à l'ordre de grandeur de la vitesse du son dans le fluide, par conséquent, en ordre de grandeur :
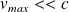
Il est donc possible d'appliquer la relation de Bernoulli la plus simple (écoulement parfait stationnaire, homogène et irrationnel) :
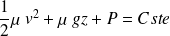
A un fluide compressible, dans la mesure où la vitesse d'écoulement reste très inférieure à la vitesse de propagation du son dans ce fluide.
Attention : Jet homocinétique à l'air libre
On considère l'écoulement stationnaire d'un fluide incompressible sous forme :
D'un jet libre, c'est-à-dire sans aucun contact avec une surface rigide ou un autre fluide
De vitesse constante
Ce jet est dit homocinétique.
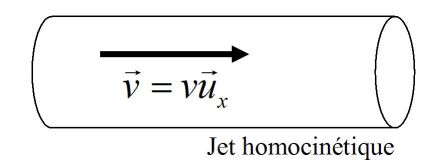
On suppose que les seules forces intervenant sont les forces de pression ; la relation de Bernoulli s'écrit, dans tout le jet :
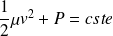
La vitesse étant la même en tout point du jet, il en est de même de la pression.
Aux bords du jet, au contact de l'atmosphère, la pression vaut
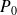. C'est donc la pression en tout point du jet.
Dans un jet homocinétique à l'air libre, la pression est uniforme et égale à celle existant dans le milieu extérieur.
On admettra ce résultat pour tout jet à l'air libre.
Exemple : Le phénomène de Venturi
Un écoulement stationnaire homogène incompressible et soumis aux seules forces de pression, est limité par une conduite de section variable.
Le problème est unidimensionnel : toutes les grandeurs ont une valeur uniforme sur une section droite de la conduite.
La conservation du débit volumique
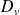entre les deux sections d'aires
et
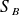donne :
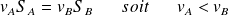
L'application du théorème de Bernoulli entre deux points A et B situés sur une même horizontale donne :
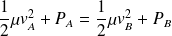
On en déduit que
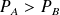: les régions de faible section, donc de grande vitesse, sont aussi des régions de basse pression (effet Venturi).
Dans les tubes verticaux, le fluide est immobile et les hauteurs de liquide mesurent les pressions
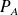et
:
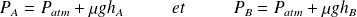
On en déduit la différence de pression :
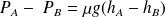
On peut ensuite en déduire le débit volumique dans la conduite, en calculant préalablement
:
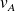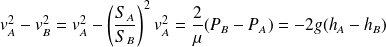
D'où :
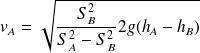
Et le débit volumique
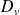vaut :
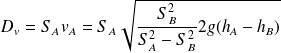
Le tube de Venturi peut ainsi servir de débitmètre.
Remarque : l'effet Venturi reste bien vérifié par un gaz compressible comme l'air, tant que sa vitesse reste inférieure à la vitesse de propagation du son.
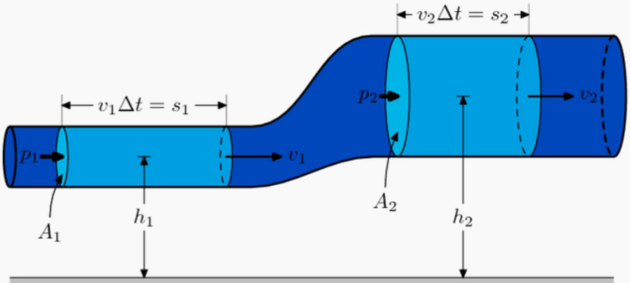
Complément : Une autre démonstration du théorème de Bernoulli
On va appliquer le principe de conservation de l'énergie le long d'une ligne de courant, en négligeant les effets thermiques ainsi que les effets de viscosité et de compressibilité du fluide.
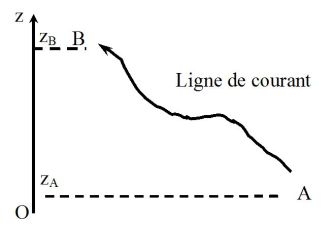
On raisonne en utilisant les notations de la figure ci-dessous.
On considère le système compris à l'instant
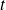entre
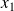et
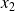et à l'instant
entre
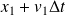et
.
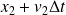Le fluide étant incompressible :
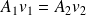et
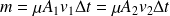
Le premier principe appliqué aux fluides en écoulement permet d'écrire : (premier principe industriel)
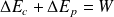
On suppose ici que l'énergie interne ne change pas (on néglige les effets thermiques) et qu'il n'y a pas de transferts thermiques (absence de viscosité).
Avec :
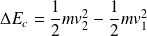
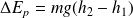
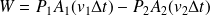(travail des forces de pression)
Ainsi :
Soit, en utilisant
:
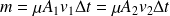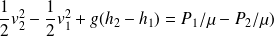
Soit finalement :
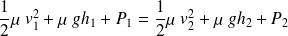
ON retrouve ainsi l'expression du théorème de Bernoulli le long d'une ligne de courant.
Exemple : Quelques vidéos d'expériences
Une balle de ping-pong récalcitrante
Faire léviter une balle de ping-pong
