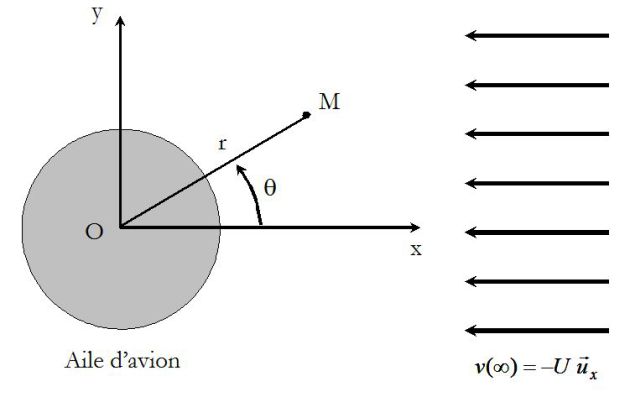
Écoulement autour d'une aile d'avion
On considère une aile d'avion cylindrique d'axe horizontal (Oz) et de rayon R, en mouvement rectiligne uniforme à vitesse
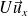 dans le référentiel terrestre (R0).
dans le référentiel terrestre (R0).
Loin de l'aile, l'air est au repos et la pression est constante (notée
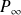 ).
).
Il est commode pour exprimer les conditions aux limites sur l'aile de traiter le problème dans le référentiel (R) lié à l'avion, où l'on note
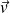 le champ eulérien des vitesses.
le champ eulérien des vitesses.
Loin de l'aile, la loi de composition des vitesses donne :
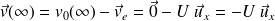
Hypothèses :
L'écoulement est stationnaire.
L'écoulement est incompressible ; ce choix est convenable bien que l'air soit un fluide compressible si l'on suppose que l'avion est subsonique (Voir rappels de cours sur le théorème de Bernoulli).
L'écoulement est irrotationnel.
L'écoulement est plan et invariant par translation le long de l'axe de l'aile (on néglige les effets de bords) et on écrit :
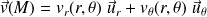
Recherche du champ des vitesses :
L'écoulement étant irrotationnel (
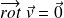 ), il existe un potentiel des vitesses
), il existe un potentiel des vitesses
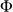 tel que :
tel que :
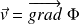
L'écoulement étant incompressible,
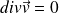 , soit
, soit
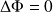 , le potentiel des vitesses vérifie l'équation de Laplace.
, le potentiel des vitesses vérifie l'équation de Laplace.
Étant donné l'invariance par translation selon (Oz), le potentiel des vitesses est de la forme
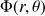 .
.
La solution générale de l'équation de Laplace est dans ce cas (résultat mathématique admis) :
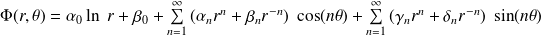
Où les
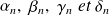 sont des constantes quelconques.
sont des constantes quelconques.
On reconnaît dans cette expression un développement en série de Fourier du potentiel des vitesses à r fixé.
Le problème étant symétrique par rapport au plan médiateur de l'aile
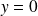 , ce développement est pair en
, ce développement est pair en
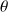 et les termes en sinus sont nuls :
et les termes en sinus sont nuls :
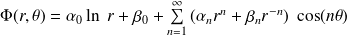
A l'infini :
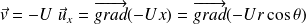
Soit
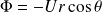
On en déduit :

Ainsi :
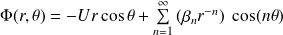
Sur l'aile, la coordonnée normale (la vitesse radiale) de la vitesse doit s'annuler :
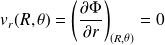
Or :
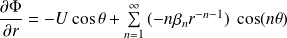
Par conséquent :
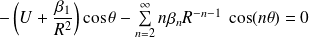
D'où :
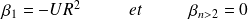
Finalement :
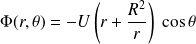

On en déduit les coordonnées du champ des vitesses :
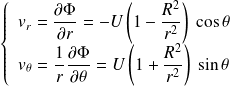
L'animation ci-dessous donne l'allure des lignes de courant autour de l'aile d'avion.
Simulation : Animation JAVA de JJ.Rousseau (Université du Mans)
Écoulement laminaire autour d'un cylindre : cliquer ICI