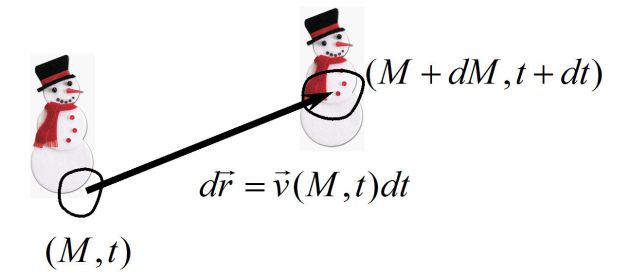Accélération particulaire
Imaginer un petit bonhomme sur une particule fluide (toujours la même) : les variations des grandeurs qu'il mesure (vitesse, pression, masse volumique, ...) sont des variations particulaires, c'est-à-dire des variations de grandeurs liées à la même particule qui se déplace au cours du temps.
On comprend intuitivement que, pour étudier le mouvement d'une particule de fluide soumise à différentes forces, il va falloir déterminer son accélération.
Mais comment calculer l'accélération d'une particule de fluide en formalisme eulérien ?
La différentielle de la vitesse d'une particule de fluide (toujours la même) vaut :
Pendant l'intervalle de temps dt, la particule de fluide s'est déplacée de :
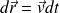
D'où :
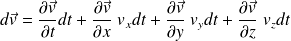
Et l'accélération de la particule de fluide devient :
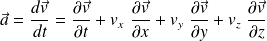
Soit encore :
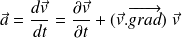
En toute rigueur,
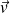dans le membre de gauche désigne la vitesse de la particule fluide (et
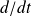est appelée dérivée particulaire, encore notée
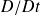) alors que dans les autres termes,
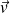désigne le champ des vitesses dans tout le fluide.
Enfin, le terme
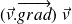permet de rendre compte que, même dans un écoulement stationnaire (dans le sens eulérien du terme), aux variations spatiales de la vitesse correspondent des accélérations pour les particules.
Attention : Accélération particulaire
-
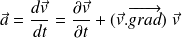
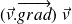: la dérivée convective, qui indique un caractère non uniforme de
.
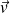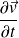: la dérivée locale, qui indique un caractère non permanent de
.
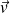On peut montrer que (se placer en coordonnées cartésiennes) :
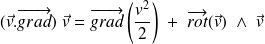
Complément : Généralisation
La dérivée particulaire d'une grandeur vectorielle quelconque
est donnée par :
On retrouve là encore la notion de dérivée convective et de dérivée locale.
De même, pour la dérivée d'une grandeur scalaire, comme la masse volumique
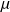par exemple :
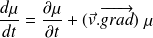
Définition : Vecteur tourbillon
Le tourbillon, parfois appelé vorticité (du latin vortex), est une formulation mathématique de la dynamique des fluides reliée à la quantité de vitesse angulaire ou de rotation que subit un fluide localement.
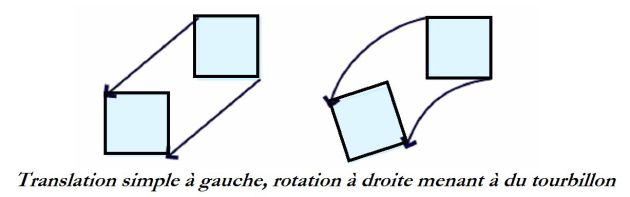
Une façon simple de visualiser le tourbillon est de considérer un fluide en mouvement dans lequel on délimite un petit volume rigide.
Si cette parcelle tourne par rapport à un référentiel au lieu de translater, elle tourbillonne.
On définit alors, pour un fluide, le vecteur tourbillon par :
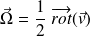
Ce vecteur représente le vecteur rotation (locale) d'une particule de fluide.
Localement, le champ des vitesses d'un fluide renseigne sur l'existence de tourbillons dans ce fluide par l'intermédiaire de son rotationnel.
Un écoulement est dit non tourbillonnaire (ou irrotationnel) si le vecteur tourbillon est nul en tout point.
Dans le cas contraire, l'écoulement est dit tourbillonnaire.
Il ne faut pas confondre turbulences et tourbillons :
Un champ des vitesses de la forme :
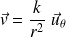
Est tourbillonnaire (comme on peut le vérifier en coordonnées cylindriques), mais il ne s'agit pas d'une turbulence.
On peut calculer le vecteur tourbillon :
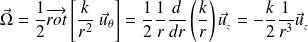
La fonction mathématique qui décrit ce champ des vitesses est « simple ».
En pratique, les turbulences sont constituées de tourbillons de taille et de forme variables, qui se font et se défont constamment.
Attention : Vecteur tourbillon
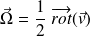
Ce vecteur représente le vecteur rotation (locale) d'une particule de fluide.
