Écoulement de Couette
Un fluide incompressible de masse volumique
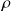et de viscosité
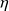, immobile entre deux plans horizontaux, est mis en mouvement par le seul déplacement du plan supérieur en
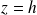à vitesse constante
.
On cherche un écoulement laminaire de la forme :
La vitesse ne dépend pas de y (invariance par translation selon Oy) et est indépendante de x car l'écoulement est incompressible.
Vu le champ des vitesses choisi, l'accélération convective est nulle.
L'équation de Navier - Stokes devient alors, en projection selon (Oz) : (et en l'absence de gradient de pression selon (Ox))
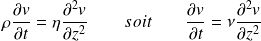
On obtient une équation de diffusion.
La mise en mouvement du fluide par la translation de la plaque supérieure atteint la profondeur
en un temps
, ordre de grandeur de la durée du régime transitoire, donné par
.
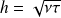Pour
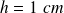et avec
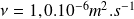, on trouve
.
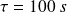Une fois le régime transitoire passé, la résolution de l'équation de diffusion donne directement :
