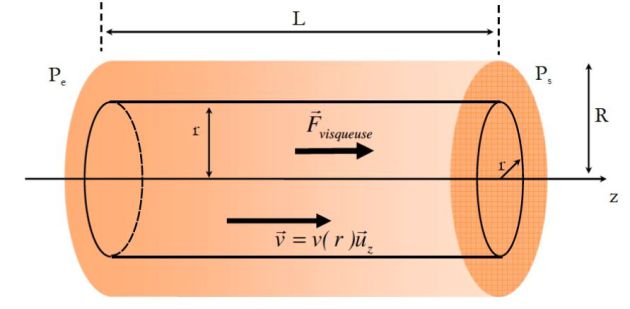
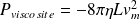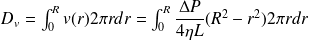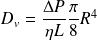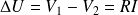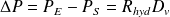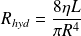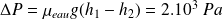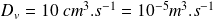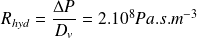Écoulement de Poiseuille
Méthode : Champs des vitesses et des pressions
En 1835 un médecin français, Poiseuille fit une série d'expériences pour déterminer comment un fluide visqueux s'écoule dans un tuyau droit.
Son but était de comprendre la dynamique de la circulation sanguine chez l'homme sachant que le plasma sanguin se comporte comme un fluide newtonien.
Un fluide visqueux incompressible de densité
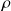s'écoule dans un tube cylindrique de longueur L et de rayon R.
La pression à l'entrée du tube (
) est
.
La pression à la sortie du tube est
.
On va calculer les champs des vitesses et de pression à l'intérieur du tube en se plaçant en régime stationnaire.
On suppose l'écoulement laminaire :
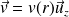
On suppose que
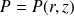(invariance par rotation autour de l'axe Oz) et la pesanteur est négligée.
L'équation de Navier - Stokes s'écrit dans ces conditions :
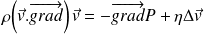
On évalue l'accélération convective :
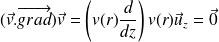
On obtient ainsi l'équation dite de Stokes :
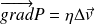
En projection sur
:
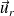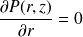
Par conséquent, la pression ne dépend que de z :
.
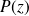En projection selon
:
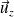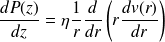
Le terme de gauche ne dépend que de z alors que le terme de droite ne dépend que de r. Par conséquent :
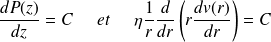
Où
est une constante.
Ainsi :
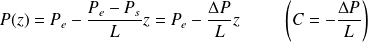
La vitesse vérifie l'équation différentielle :
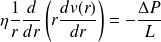
Après une double intégration et en éliminant le terme qui diverge en
, on obtient, en utilisant les conditions aux limites (vitesse du fluide nulle en
) :
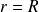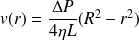
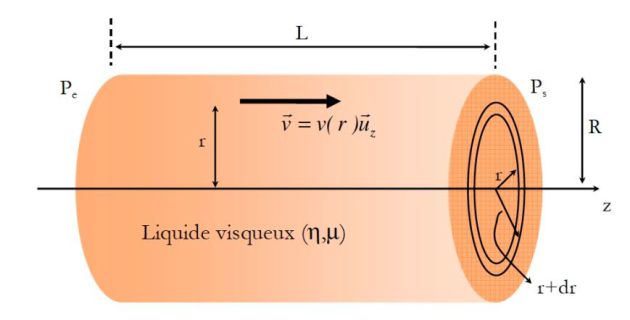
La courbe ci-dessus donne le profil parabolique du champ des vitesses ainsi que la variation affine de la pression.
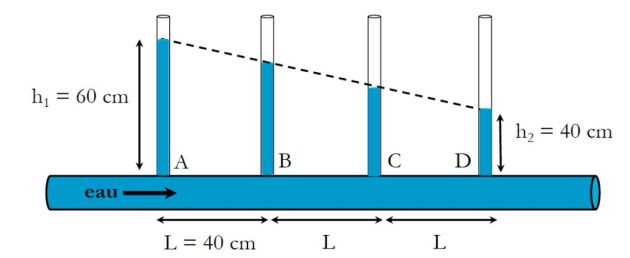
On appelle "perte de charge" la quantité
.
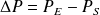Méthode : Débit volumique
Le débit volumique vaut ici :
Soit :
On définit une "résistance hydraulique", par analogie avec une résistance ohmique (
) :
Soit :
La résistance hydraulique est d'autant plus élevée que la viscosité du fluide est grande et que le rayon du tube est petit.
Complément : Bilan de quantité de mouvement
On applique le théorème de la résultante cinétique au système constitué du fluide contenu dans le cylindre de rayon
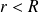à l'instant t et de la masse
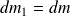qui y rentre entre
et
.
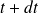A l'instant
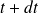, ce système est constitué du fluide contenu dans le cylindre de rayon
à
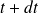et de la même masse
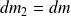qui en sort entre
et
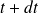(écoulement incompressible).
Si l'on se place dans le cadre du régime permanent, la variation de quantité de mouvement du système est alors simplement nulle.
Le bilan des forces s'écrit alors :
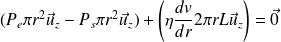
D'où :
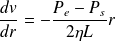
Par intégration, en tenant compte de
:
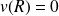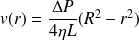
On retrouve bien l'expression de la vitesse de l'écoulement obtenue à partir de l'équation de Navier – Stockes.
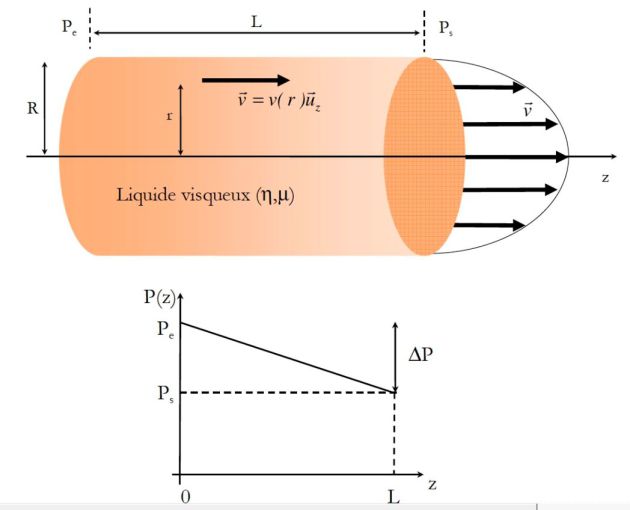
On peut, par un raisonnement énergétique, déterminer la puissance des forces de viscosité qui s'applique sur la conduite.
En régime permanent, la variation d'énergie cinétique du système précédent est nulle, par conséquent, en termes de puissance :
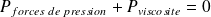
Soit :
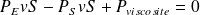
D'où :
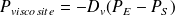
On définit la vitesse moyenne
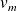de l'écoulement par :
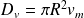
D'où (avec
) :
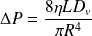Exemple : Perte de charge et résistance hydraulique
On place une succession de tubes verticaux le long de la conduite.
La mesure des hauteurs d'eau permet de déterminer la perte de charge :
Si le débit est
, on peut en déduire la résistance hydraulique :
