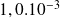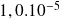Équation de Navier-Stokes
Rappel : Forces surfacique de viscosité
On étudie un cas simple où les plans parallèles à (Oxz) glissent les uns sur les autres (voir figures).
Ce cas est une bonne approximation de la réalité lorsque les dimensions de l'écoulement selon (Ox) et (Oz) sont grandes vis-à-vis de l'épaisseur de la couche de fluide.
On suppose que le vecteur vitesse peut s'écrire sous la forme (voir figure) :
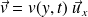
Comme
, cet écoulement peut être celui d'un fluide incompressible.
Considérons deux éléments de fluide S1 et S2, séparés par la surface S, d'aire S et normale à (Oy).
La force de cisaillement, exercée par S2 sur S1, est tangente à S.
Dans le cas de la figure, la surface S2 va plus vite que la surface S1 et va donc l'entraîner avec elle.
Cette force est donc :
Proportionnelle à l'aire S de la surface S.
De même sens que
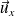si
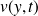est une fonction croissante de
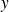.Pour un fluide dit "newtonien", la force de cisaillement est une fonction linéaire de la dérivée
.
Finalement, pour un écoulement unidirectionnel, tel que
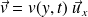, la force de surface tangentielle
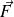, appelée force de cisaillement ou de viscosité, qui s'exerce à travers une surface d'aire S normale à vaut
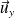(il s'agit de la force exercée par la couche supérieure sur la couche inférieure) s'exprime ainsi :
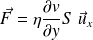
La viscosité a pour effet, dans un écoulement unidirectionnel, d'accélérer les éléments lents et de freiner les éléments rapides.
Il s'agit donc d'un transfert interne de quantité de mouvement, qui présente les caractéristiques d'une diffusion de quantité de mouvement.
Le coefficient
, appelé coefficient de viscosité du fluide, peut être, avec une bonne approximation, considéré comme une constante caractéristique du fluide à une température donnée.
L'unité pour le coefficient de viscosité est le poiseuille (symbole Pl, égal à 1 Pa.s).
Quelques exemples (dans les conditions normales) :
Corps pur | Eau | Air | Glycérine |
Viscosité (Pl) |
|
|
|
Attention : Forces surfacique de viscosité
Pour un écoulement unidirectionnel, tel que :
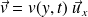
La force de surface tangentielle
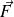, appelée force de cisaillement ou de viscosité, qui s'exerce à travers une surface d'aire S normale à vaut
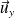(il s'agit de la force exercée par la couche supérieure sur la couche inférieure) s'exprime ainsi :
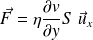
Équivalent volumique des forces de viscosité
On considère un « pavé » de fluide de volume
.
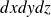On suppose que le champ des vitesses peut encore s'écrire sous la forme :
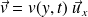
Pour un tel champ, les forces de viscosité sont portées par l'axe (Ox) et seules les faces
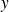et
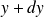sont concernées.
On peut écrire, en appliquant le principe de l'action et de la réaction, la résultante des forces de viscosité sur le pavé de fluide :
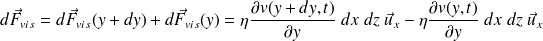
Soit :
Pour un champ des vitesses quelconque mais correspondant à un écoulement incompressible, nous admettrons que ce résultat se généralise sous la forme :
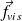est la densité volumique des forces de viscosité ; elle n'est qu'un équivalent mathématique car ces forces ne s'appliquent qu'à la surface d'un système.
Attention : Équivalent volumique des forces de viscosité
Pour un champ des vitesses quelconque mais correspondant à un écoulement incompressible, la densité volumique des forces de viscosité est :
Équation de Navier-Stokes
Le principe fondamental de la mécanique appliqué à une particule de fluide, en tenant compte de la force de viscosité conduit à l'équation de Navier – Stokes :
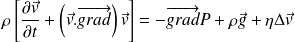
C'est l'équation de Navier - Stokes.
Ou encore :
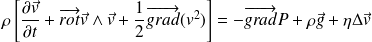
Rappelons que :
Fluide incompressible :
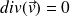
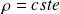
La condition portant sur la vitesse à l'interface fluide - solide est :
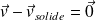
Attention : Équation de Navier-Stokes
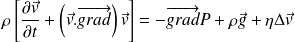
C'est l'équation de Navier - Stokes.
Ou encore :
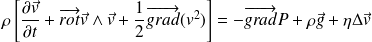
Complément : Liquides newtoniens et liquides non newtoniens
Écoulements du miel et du dentifrice
