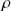Naufrage d'un bateau
15 minutes de préparation)
On considère un bateau qui coule dans la mer considérée comme un fluide parfait incompressible, de masse volumique
.
On note
la hauteur du bateau,
sa masse et
sa surface de base.
Question
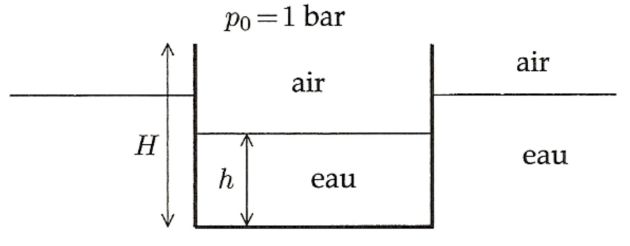
On considère que le bateau est rempli d'eau sur une hauteur
.
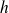Quelle est la hauteur
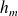à partir de laquelle le bateau coule ?
On appelle
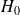la hauteur du bateau qui se trouve dans l'eau.
A l'équilibre du bateau, les poids du bateau et de la masse d'eau de hauteur
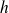compensent la poussée d'Archimède (axe vertical orienté vers le haut) :
On en déduit :
La bateau va couler si
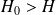, d'où la hauteur limite :
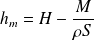
L'AN donne
.
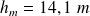Question
On considère maintenant que le bateau est initialement vide et qu'il se remplit par un petit trou de surface
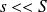situé dans la coque à une hauteur
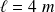du fond.
On prendra
.
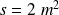Décrire les différentes étapes du remplissage.
Déterminer
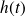pendant la 1ère phase et calculer sa durée
.Déterminer
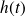pour
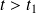.Quelle est la durée totale du naufrage ?
Le remplissage va se dérouler en deux étapes : le niveau d'eau monte juste au niveau du trou puis le niveau d'eau monte jusqu'à atteindre la hauteur
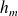.Ensuite, le bateau va couler ...
Étude de la 1ère phase :
On note
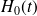la hauteur du bateau dans l'eau, qui dépend du temps. On applique le théorème de Bernoulli (dans l'ARQS) pour déterminer la vitesse de l'eau
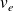à l'entrée du trou dans le référentiel du bateau, sur une ligne de courant allant de la surface de la mer au trou. On a alors :
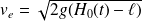
La conservation du débit volumique donne ensuite :
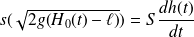
où
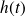désigne la hauteur d'eau à l'instant t dans le bateau.On va considérer que le bateau est pratiquement immobile, ce qui fait que l'on peut encore écrire (comme à la question précédente) :
Par conséquent :
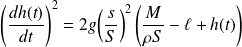
On dérive par rapport au temps et, après simplifications :
Les conditions initiales sont :
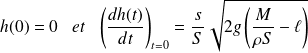
On obtient, après intégration :
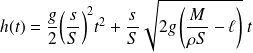
La 1ère phase va se terminer à l'instant
pour lequel
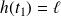, soit :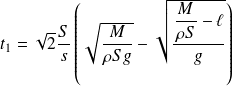 
L'AN donne :
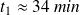
Étude de la seconde phase :
On utilise de nouveau le théorème de Bernoulli entre la surface de la mer et le trou situé au point E. La pression vaut maintenant, au niveau du trou :
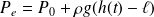
Ainsi :
D'où, finalement :
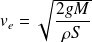
Cette vitesse est donc constante.
La conservation du débit volumique conduit à :
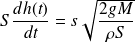
La résolution de cette équation différentielle donne :
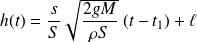
La seconde phase se termine lorsque
. L'AN donne :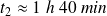 
C'est la durée du naufrage.
