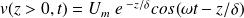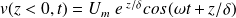Freinage d'une plaque en mouvement sinusoïdal
(20 minutes de préparation)
Une plaque confondue avec le plan d'équation z = 0 est en translation avec une vitesse
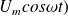dans un fluide incompressible de masse volumique
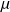, de viscosité
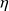et de viscosité cinématique
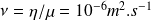, remplissant tout l'espace.
On considérera la plaque comme infinie.
On note alors
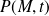le champ de pression et
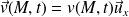le champ des vitesses en M, dans le fluide.
On rappelle l'expression de la force de viscosité exercée sur un élément de surface dS, de cote z, par le fluide situé à une cote supérieure à z :
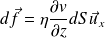
Question
De quoi dépendent
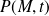et
?
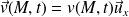On montrera avec soin que
.
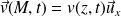L'équation de Navier-Stokes conduit ici à l'équation de diffusion.
La résolution fait apparaître une épaisseur de peau, comme en électromagnétisme (dans les conducteurs ohmiques) et comme dans les transferts thermiques (voir exercice sur l'onde thermique)
Il y a invariance par translation selon Ox et Oy, par conséquent : P(z,t) et
.
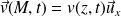Question
En isolant un pavé de côtés dx, dy et dz dont un coin est le point M de coordonnées (x,y,z), établir l'équation :
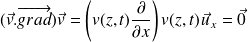
L'équation de Navier-Stokes donne, en projection selon (Ox) la relation demandée (équation de diffusion) :
Question
En déduire sans calculs l'ordre de grandeur de l'épaisseur
de la couche limite, domaine hors duquel le fluide reste quasiment au repos.
Application numérique pour f = 100 Hz.
Un calcul d'ordre de grandeur donne, où V est un ordre de grandeur de la vitesse du fluide :
D'où :
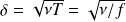
Question
On cherche en régime sinusoïdal forcé un champ des vitesses de la forme :
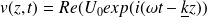
Déterminer le vecteur d'onde complexe
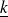et les expressions des vitesses
et
.
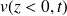L'équation de diffusion donne la relation de dispersion :
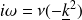
Soit :
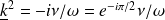
D'où l'expression du vecteur d'onde complexe :
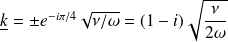
On note finalement :
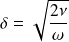
En prenant la partie réelle, on en déduit les expressions des vitesses dans le plan supérieur et dans le plan inférieur :
Question
En déduire l'expression de la force subie par la plaque de surface S et la puissance moyenne de cette force ; commenter.
La force subie par la plaque de surface S est la force de viscosité :
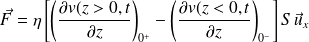
Soit :
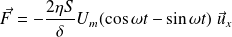
La puissance moyenne est :
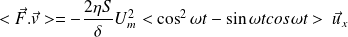
Soit :
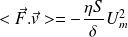
L'opérateur doit donc fournir la puissance opposée afin d'assurer le mouvement en régime permanent de la plaque freinée par le liquide visqueux.
