Film de peinture
(20 minutes de préparation)
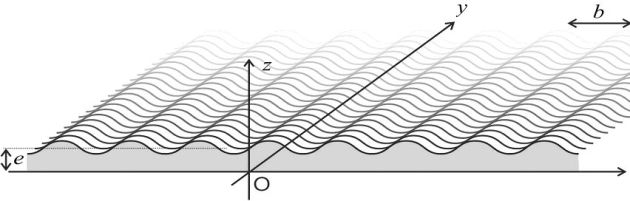
On étudie l'évolution d'un film de peinture d'épaisseur e (selon Oz), après un coup de pinceau sur une surface horizontale, les poils laissant des stries distantes de b (selon Ox).
La peinture est assimilée à un fluide newtonien incompressible de viscosité
et de masse volumique
:
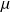Question
Justifier la forme de la vitesse :
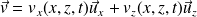
Montrer que
.
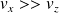Dans la suite, la composante verticale de la vitesse est négligée. On propose une solution de la forme :
Les forces de pression et le poids sont négligés devant les forces de viscosité.
Il y a invariance selon Oy. Le fluide étant incompressible
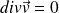, soit :
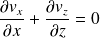
On effectue un calcul d'ordre de grandeur :
Comme
,
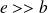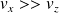
Question
Exprimer les conditions aux limites en z = 0 et z = e.
Les conditions aux limites sont :
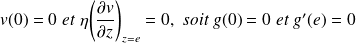
Question
Montrer que l'accélération convective est négligeable devant les autres termes de l'équation de Navier Stockes.
On effectue de nouveau un calcul d'ordre de grandeur :
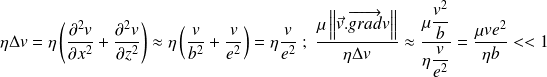
Question
Déterminer l'équation différentielle vérifiée par g(z). Déterminer
, commenter.
L'équation de Navier – Stockes devient simplement :
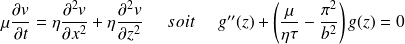
La solution est de la forme :
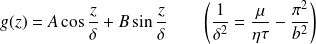
Comme
,
.
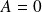La condition
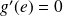conduit à :
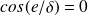
Soit :
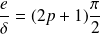
Ce qui permet de connaître la valeur de
.
