Ondes dans un bassin
(20 minutes de préparation)
On considère un fluide parfait incompressible (de masse volumique
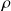) dans un bassin de largeur L (selon Oy).
Une onde se propage selon (Ox). Le champ des vitesses est de la forme :
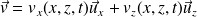
La pression
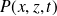est hydrostatique dans le canal.
On note
la hauteur de l'eau dans le canal (H est une constante).
L'écoulement est supposé irrotationnel.
Question
Appliquer l'équation d'Euler à une particule de fluide. Trouver une équation différentielle entre
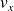et
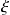dans l'hypothèse des petits mouvements.
Montrer que
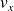est indépendante de z.
L'équation d'Euler s'écrit :
La pression est hydrostatique, ce qui signifie qu'elle est donnée par l'expression obtenue en statique des fluides, soit :
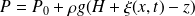
Dans l'hypothèse des petits mouvements, on ne garde que les termes du 1er ordre (approximation semblable à l'approximation acoustique pour l'étude des ondes dans les fluides).
L'équation d'Euler devient alors :
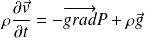
En projection selon l'horizontale, on obtient l'équation différentielle entre
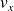et
:
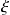Soit :
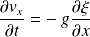
L'écoulement est incompressible, donc :
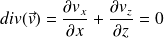
En ordre de grandeur, si on note λ la longueur d'onde de l'onde (dans la direction (Ox)) et a une dimension caractéristique du mouvement vertical (avec
) :
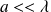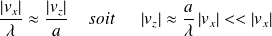
On pourra donc négliger la composante verticale de la vitesse.
L'écoulement est irrotationnel :
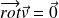
Ce qui conduit à, en négligeant
:
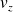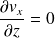
Par conséquent,
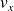ne dépend pas de z.
Question
Calculer le débit volumique
.
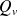Faire un bilan de masse sur une tranche d'épaisseur dx.
En déduire une équation différentielle entre
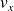et
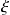dans l'hypothèse des petits mouvements.
Le débit massique est :
Bilan de masse sur une tranche d'épaisseur dx, située entre x et x+dx :
Soit dm la variation de masse dans cette tranche. On peut l'écrire de deux manières :
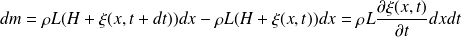
Ou encore :
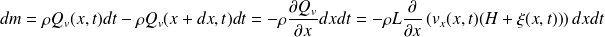
Par identification :
Au 1er ordre :
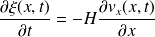
Question
Montrer que
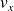et
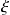vérifient chacun une équation de propagation classique.
En déduire la vitesse de propagation des ondes dans le canal.
On a ainsi les deux équations :
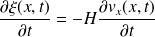
Et :
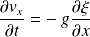
En découplant ces deux équations, on aboutit à l'équation de d'Alembert :
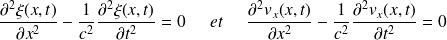
Où la vitesse de propagation de l'onde est :
