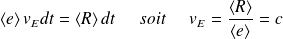Étude énergétique d'une corde vibrante
(30 minutes de préparation)
Soit une corde de masse linéique
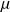tendue par une tension T0 horizontale au repos.
Question
Donner l'équation aux dérivées partielles vérifiée par l'élongation verticale y(x,t). Quelle est la célérité des ondes ?
Voir le cours :
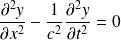
Et la vitesse des ondes est :
Question
Donner l'énergie cinétique ec de la corde par unité de longueur.
L'énergie cinétique ec de la corde par unité de longueur est :
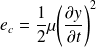
Question
Montrer que l'énergie potentielle d'un élément de corde dx est
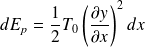
En déduire l'énergie potentielle linéique ep et l'énergie linéique totale.
La longueur de l'élément de corde dx au repos devient :
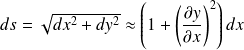
Le travail que doit fournir un opérateur pour faire passer la corde de la longueur dx à la longueur ds est :
Où Ep est l'énergie potentielle de la corde. L'énergie potentielle linéique est alors :
L'énergie linéique totale est donc :
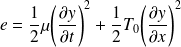
Question
Trouver la fonction R(x,t) telle que :
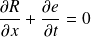
Quelle est la dimension de R et son sens physique ?
Effectuer une analogie électromagnétique.
Retrouver l'expression de R(x,t) par une autre méthode.
On évalue :
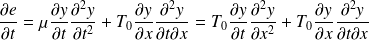
Soit :
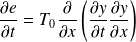
D'où :
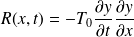
R est homogène à une puissance.
On remarque que :
C'est la puissance de la force de tension exercée par la gauche sur la droite.
On retrouve cette relation par la démonstration suivante : (équivalente à un bilan en EM ou en mécanique des fluides)
Soit :
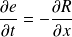
Question
Calculer la variation de l'énergie totale de la corde en fonction de R(0) et de R(L).
Que peut – on dire si la corde est attachée aux deux bouts ?
On intègre sur la longueur de la corde :
Si la corde est attachée aux deux bouts, alors l'énergie de la corde est une constante.
Question
Dans le cas d'une onde progressive sinusoïdale, calculer
,
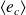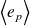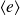et
et
.
Quelle est la vitesse de l'énergie ?
Pour une OPPH (qui se propage dans le sens positif) :
Alors :
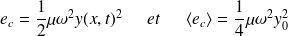
Ainsi :
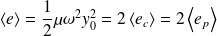
De même :
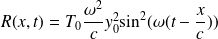
Et :
La vitesse de l'énergie est vE, donnée par le bilan classique vu en EM notamment :
