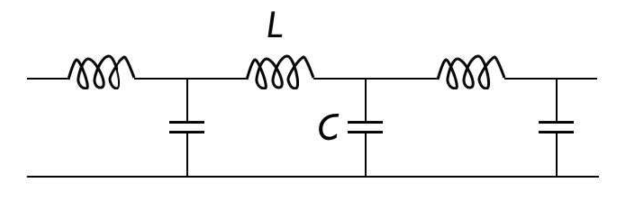
Transmission le long d'un réseau LC
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On considère la ligne de transmission ci-dessous :
Question
Déterminer la relation de dispersion pour une onde périodique traversant la ligne.
Quelle est la fréquence de coupure ?
Écrire les lois de Kirchoff.
On peut aussi utiliser le théorème de Millman.
Soit
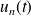la tension aux bornes du condensateur
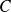de la
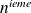cellule et
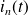le courant dans la bobine qui suit, on peut écrire :
Lois des mailles :
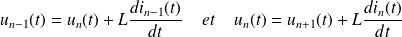
Loi des nœuds :
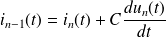
On dérive la dernière équation par rapport au temps :
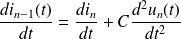
Et on utilise les deux lois des mailles :
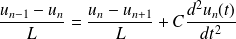
D'où :
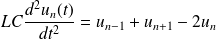
On s'intéresse à la propagation d'ondes planes que l'on écrira sous la forme :
où a est la "largeur" d'une cellule.
L'équation différentielle précédente devient alors :
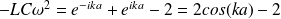
Soit, finalement :
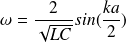
C'est la relation de dispersion demandée.
La pulsation de coupure est obtenue quand le
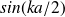est égal à 1 :
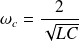
Question
Déterminer l'équation de propagation vérifiée par la tension aux bornes des condensateurs dans le cadre de l'approximation des milieux continus.
On suppose que la distance entre les cellules
est petite devant la longueur d'onde (
.
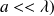On peut alors définir une fonction
telle que (développement de Taylor-Young au second ordre) :
Et l'équation de propagation devient alors :
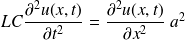
Soit :
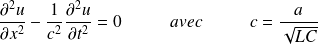
On retrouve une équation de d'Alembert, caractéristique d'une propagation sans dissipation à la vitesse c.
Complément :
On reprend la relation de dispersion obtenue à la première question :
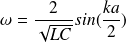
Et on suppose que
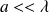(hypothèse des milieux continus).
Alors :
et, par conséquent :
La vitesse de phase (égale ici également à la vitesse de groupe) vaut alors :
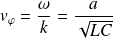
On retrouve bien la vitesse de l'onde obtenue à la deuxième question.
