Propagation du son dans les solides
Chaîne infinie d'oscillateurs et approximation des milieux continus
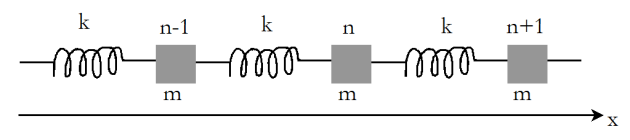
Afin d'étudier la propagation d'ondes sonores dans les solides, on utilise le modèle suivant (voir figure) :
Le solide est constitué d'une chaîne infinie d'atomes ponctuels, de masse m, reliés entre eux par des ressorts de raideur k et de longueur à vide a (correspondant à la distance inter-atome à l'équilibre).
La chaîne d'atomes couplés élastiquement (rappel linéaire) par des ressorts constitue une modélisation simple pour décrire la propagation de petits mouvements vibratoires dans un solide, c'est-à-dire la propagation du son dans un solide.
Ce dernier est en effet constitué d'empilements réguliers d'atomes (ions ou molécules).
Les forces rappelant un atome vers sa position d'équilibre peuvent être modélisées, à l'ordre linéaire, par un rappel élastique, dans la mesure où les amplitudes des vibrations des atomes sont faibles (on suppose ici que le solide est homogène et isotrope).
Le mouvement de l'ensemble se fait sans frottements le long de l'axe (Ox).
Les atomes se déplacent légèrement autour de leurs positions d'équilibres respectives, que l'on peut repérer sous la forme
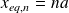 .
.
On repère les positions des atomes hors équilibre par leurs abscisses :
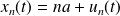
où les déplacements
 restent faibles vis-à-vis de a.
restent faibles vis-à-vis de a.
Le théorème du CI appliqué à l'atome de rang (n) donne, en projection :

La distance a inter-atome est de l'ordre de
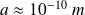 , distance très inférieure aux distances caractéristiques des phénomènes de propagation que l'on étudie, notamment vis-à-vis de la longueur d'onde de la vibration (de l'ordre de 25 cm à 20 kHz). Par conséquent,
, distance très inférieure aux distances caractéristiques des phénomènes de propagation que l'on étudie, notamment vis-à-vis de la longueur d'onde de la vibration (de l'ordre de 25 cm à 20 kHz). Par conséquent,
 varie très peu sur la distance a.
varie très peu sur la distance a.
On va ainsi définir une fonction continue u de la manière suivante : (approximation des milieux continus)
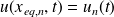
Il vient alors (développement de Taylor-Young au second ordre) :

Et l'équation du mouvement devient alors :
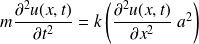
Soit :

C'est l'équation d'onde de d'Alembert, déjà obtenu en EM lors du chapitre sur les équations locales.
On sait qu'elle est associée à un phénomène ondulatoire de célérité c.
Cette vitesse ne doit pas être confondue avec la vitesse de déplacement longitudinal des atomes
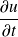 .
.
Les ondes sont ici longitudinales car le mouvement des atomes se fait dans la direction de propagation.
Définition : Lien avec le module de Young
Loi phénoménologique de Hooke :
La force dF qu'il faut exercer perpendiculairement à une surface dS d'un solide pour provoquer un déplacement u(x,t) est :

où Y désigne le module de Young.
On peut exprimer Y en fonction des grandeurs microscopiques définies dans la partie (a), soit k, m et a.

Pour cela, on considère un modèle de solide tridimensionnel constitué de chaînes d'atomes associées en parallèle de telle sorte qu'à l'équilibre les atomes soient situés aux sommets d'un réseau cubique de pas a et d'axe (Ox), (Oy) et (Oz).
Dans un tel réseau, chaque cube de côté a contient 8 atomes placés sur ses 8 sommets, chaque atome étant commun aux 8 cubes qui se touchent en ce point.
Il y a donc
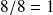 atome de masse m par cube de volume
atome de masse m par cube de volume
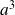 , ce qui permet d'exprimer la masse volumique du solide :
, ce qui permet d'exprimer la masse volumique du solide :
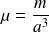
On considère une déformation du solide le long de (Ox) telle que les atomes situés en
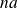 à l'équilibre soient en
à l'équilibre soient en
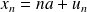 un en présence de la déformation.
un en présence de la déformation.
Soit une surface dS de ce solide découpée dans le plan d'abscisse
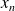 .
.
La force exercée par l'atome
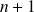 d'une chaîne sur l'atome
d'une chaîne sur l'atome
 vaut :
vaut :

La surface dS contient
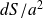 chaînes d'atomes jouant le même rôle.
chaînes d'atomes jouant le même rôle.
Donc la force exercée par la partie de solide située à droite de dS sur la partie située à gauche s'écrit :
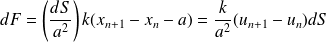
Dans l'approximation des milieux continus :
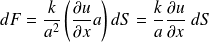
On démontre ainsi la loi de Hooke, avec le module de Young égal à :
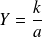
On remarque que Y est homogène à une force par une surface, soit une pression.
La vitesse de propagation du son dans le solide peux s'exprimer en fonction de Y. Les relations :
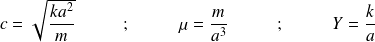
donnent finalement :
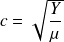
Complément : Étude mésoscopique
On peut obtenir l'équation de d'Alembert par une étude mésoscopique directe du matériau élastique étudié.
Pour cela, on prend une tranche de matériau d'épaisseur au repos
 , de surface
, de surface
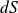 et donc de masse
et donc de masse
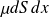 .
.
Elle subit, d'après la loi de Hooke, une force dF(x +dx,t) en x + dx et, par action et réaction, une force – dF(x,t) en x (l'élément différentiel pour les forces n'est pas relatif à l'épaisseur élémentaire dx, mais à la surface élémentaire dS).
Le PFD donne :
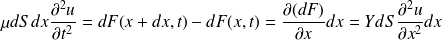
d'où l'équation d'onde :
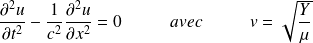
Applications numériques :
Pour
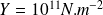 et
et
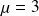 à
à
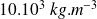 , on a
, on a
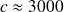 à
à
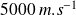 , ordre de grandeur des vitesses des ondes acoustiques des ondes dans un solide.
, ordre de grandeur des vitesses des ondes acoustiques des ondes dans un solide.