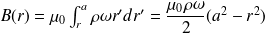Rotation uniforme d'un cylindre chargé en volume
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Soit C un cylindre de révolution d'axe (Oz), de rayon a et de longueur très grande devant a.
C, chargé uniformément avec la densité volumique ρ, est mis en rotation autour de (Oz) avec la vitesse angulaire ω (supposée indépendante du temps) sans que cette rotation affecte la répartition des charges dans C.
Question
Déterminer dans tout l'espace le champ électrique
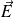 .
.
On utilise le théorème de Gauss : (le champ électrique est radial)
Pour
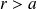 :
:
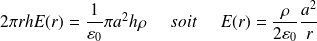
Pour
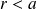 :
:
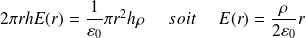
On vérifie que le champ électrique est continu à la traversée du cylindre (en r = a).
Question
Déterminer dans tout l'espace le champ magnétique
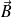 .
.
Les courants sont orthoradiaux. Utiliser le raisonnement suivi pour un solénoïde classique.
On utilise le théorème d'Ampère :
Le champ magnétique est selon l'axe du solénoïde et on sait qu'il est nul à l'extérieur.
On choisit un contour rectangulaire dont un côté parallèle à l'axe est dans le solénoïde et un autre à l'extérieur.
Alors, pour
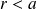 :
: