Potentiel de Yukawa
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On considère une distribution de charge ayant la symétrie sphérique autour d'un point fixe O.
Le potentiel est donné à une distance r par l'expression (Potentiel de Yukawa) :
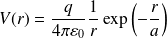
où q et a sont des constantes positives.
Question
Calculer le champ E à une distance r de O ; examiner les cas particuliers r << a et r >> a ; quelle est la signification de a ?
Le champ électrique est :
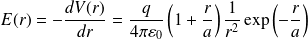
On remarque que, pour r<<a :
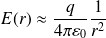
On retrouve le champ créée par une charge ponctuelle q placée en O.
Et, pour r>>a :
Vu de "loin", le champ est nulle et la distribution de charges globalement neutre.
a représente ici l'ordre de grandeur de la dimension de l'atome, c'est le rayon de Bohr.
Question
Calculer le flux φ(r) sortant d'une sphère de rayon r et en déduire que la distribution de charges est équivalente à une charge ponctuelle placée en O et à une répartition volumique de charges caractérisée par ρ(r), que l'on déterminera.
Le flux est donné, en symétrie sphérique, par :
Soit :
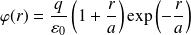
On considère le volume compris entre deux sphères de rayon
et
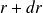. Le théorème de Gauss appliqué à ce volume donne :
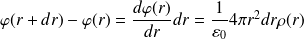
Soit :
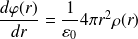
D'où l'expression de la densité volumique de charges, censée représenter l'électron de manière semi-quantique :
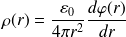
Soit :
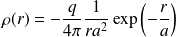
Remarque :
La charge
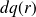comprise dans le volume compris entre deux sphères de rayon
et
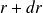est :
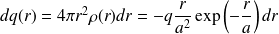
On définit la densité linéique de charges (équivalente à la densité de probabilité en mécanique quantique) :
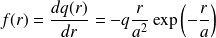
Calculons sa dérivée :
On voit que
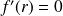pour
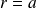et on peut vérifier qu'il s'agit d'un maximum.
On voit ainsi que l'électron est "essentiellement" réparti autour du rayon de Bohr, rayon qui correspond à la trajectoire circulaire classique de l'électron dans un modèle planétaire d'atome.
