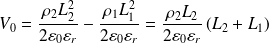Étude d'une diode à jonction
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
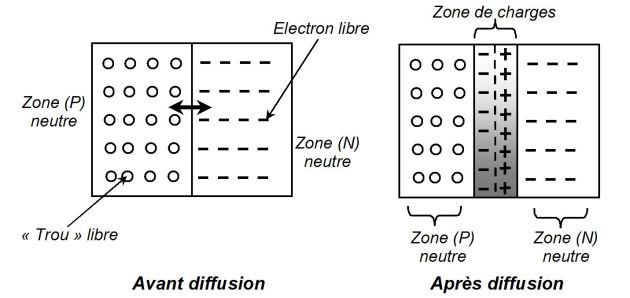
Lorsque deux semi-conducteurs de types différents P et N sont accolés (figures ci-dessous), les porteurs majoritaires des deux régions, de signe électrique contraire, s'attirent (phénomène de diffusion).
Ainsi, dans le cristal dopé N qui a perdu quelques uns de ses électrons, apparaît près de la jonction une charge volumique positive, alors que de l'autre côté de la jonction, dans le cristal dopé P, se développe au contraire une charge volumique négative.
Ces charges ne peuvent se recombiner puisqu'elles sont liées au réseau cristallin et qu'elles ne sont pas libres.
La barrière de potentiel qui se crée alors au niveau de la jonction (encore appelée tension de seuil) fait cesser ensuite cette diffusion.
Une telle jonction P-N est appelée diode à semi-conducteurs. Les propriétés qui en résultent sont à la base de la caractéristique des transistors et de tous les circuits intégrés.
Le but de cet exercice est d'étudier cette distribution de charges électriques non nulle qui apparaît au niveau de la jonction, dans une région appelée « zone de charges ».
Question
On considère un plan infini d'équation z = 0, portant une densité surfacique de charges
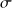constante.
Ce plan est plongé dans un milieu quasi isolant dans lequel la permittivité électrique du vide ε0 doit être simplement remplacée, notamment dans l'expression du théorème de Gauss pour le champ électrique, par le produit ε0εr, où εr est la permittivité relative du milieu considéré.
Déterminer le champ électrique en un point M quelconque de l'espace créé par ce plan infini.
On peut appliquer le théorème de Gauss de manière locale ou intégrale.
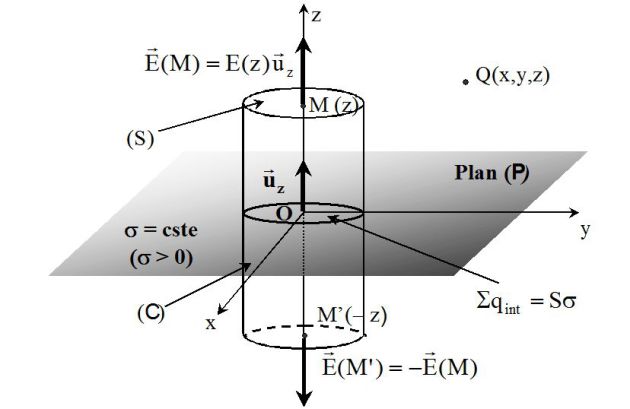
1. Soit un point Q quelconque de l'espace ; la distribution de charges sur le plan (P) étant invariante par translation selon les axes (Ox) et (Oy), le champ électrique dû à ce plan ne dépend pas des coordonnées x et y de Q.
Il suffit donc de calculer le champ en un point M situé sur l'axe (Oz), de cote z.
Tous les plans contenant l'axe (Oz) (et donc le point M) sont plans de symétrie positive pour la répartition de charges ; ainsi, le champ électrique en M, inclus dans tous ces plans, est finalement porté par l'axe (Oz), soit .
Par ailleurs, le plan (Oxy) est un plan de symétrie positive pour la répartition de charges, par conséquent les champs aux points M(z) et M'(-z) sont symétriques l'un de l'autre par rapport au plan (Oxy).
Autrement dit,
, soit
.
Le théorème de Gauss permet de déterminer le champ au point M.
Soit (C) le cylindre de hauteur 2z, de section transverse (S) et dont les bases passent par les points M(z) et M'(-z), alors (voir figure) :
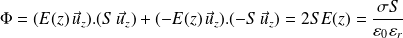
D'où :
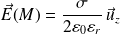
Question
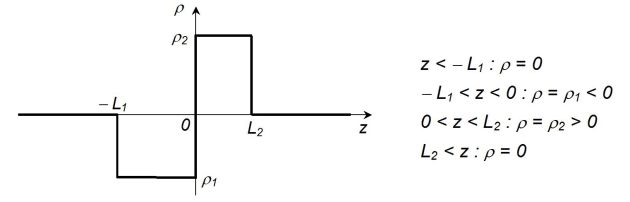
On se place dans le germanium, de permittivité relative εr, et on suppose que la densité volumique de charges ρ, autour d'une jonction située dans le plan z = 0, a l'allure donnée sur la figure ci - dessous.
La jonction est suffisamment large pour supposer que la distribution de charges est totalement invariante par toute translation dans le plan (Oxy).
Sachant que la distribution de charges est globalement neutre, établir la relation vérifiée par L1, L2, ρ1 et ρ2.
La distribution de charges étant globalement neutre :
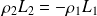
Question
Déterminer le champ électrique
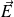en tout point M de l'espace.
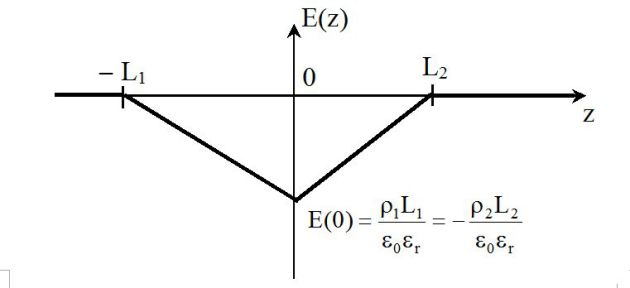
Représenter graphiquement la valeur algébrique du champ électrique en fonction de z.
Le champ en un point quelconque de l'espace est encore porté par l'axe (Oz) et, comme à la question précédente, il suffit de s'intéresser au champ en un point M de l'axe (Oz), que l'on note :
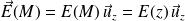
En un point extérieur (en M3 ou en M4, voir figure) à la zone de charges, le champ électrique est équivalent à celui créé par une succession de plans infinis chargés collés les uns aux autres, de densités surfaciques
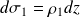et
.
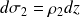Le champ résultant au point M3 par exemple est, en vertu du principe de superposition et en utilisant le résultat de la question (1) :
Par conséquent, en utilisant la condition de neutralité électrique de la jonction,
.
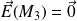Il en est de même pour le point M4,
.
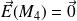Le champ électrique est ainsi nul en dehors de la zone de charges.
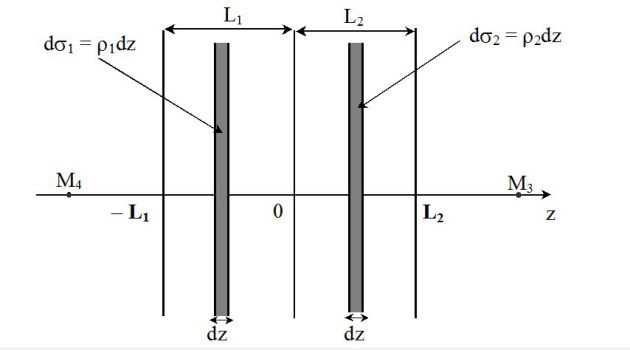
Soit le point M2 compris dans la zone chargée ρ2 ; le théorème de Gauss permet d'écrire, en prenant comme surface de Gauss un cylindre d'axe (Oz), dont la base de gauche contient M2 et dont la base de droite (voir figure ci-dessous) se trouve dans la zone où le champ est nul :
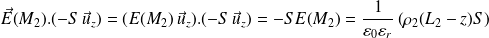
D'où :
(Pour
)
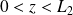Soit désormais le point M1 compris dans la zone chargée ρ1 ; de la même manière :
Alors :
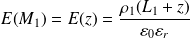(Pour
)
La représentation graphique de E(z) est donnée sur la figure ci-dessus : on remarque (propriété des répartitions volumiques de charges) que le champ est continu en z=0.
Question
En déduire le potentiel électrostatique V(M). On choisira l'origine des potentiels dans le plan z = 0.
Donner l'expression de la différence de potentiel V0 entre deux points situés de part et d'autre de la zone de charges.
Le potentiel électrostatique V(z) se détermine d'une part à partir de la relation intrinsèque entre le champ et le potentiel :
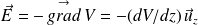
Et d'autre part à partir de la continuité du potentiel en
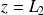et
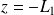. On obtient alors, en imposant au potentiel la valeur nulle dans le plan
:
Pour
:
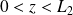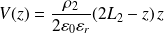
Pour
:
Pour
:
Pour
:
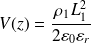
La différence de potentiel V0 entre deux points situés de part et d'autre de la zone de charges devient alors, avec de plus
:
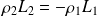