Câble coaxial
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On considère un câble coaxial infini cylindrique, de rayons R1 < R2 < R3.
Le courant d'intensité totale I passe dans un sens dans le conducteur intérieur et revient dans l'autre sens par le conducteur extérieur.
On suppose que le courant est réparti de manière volumique et uniforme dans le conducteur intérieur et de manière surfacique dans le conducteur extérieur.
Question
Calculer le champ magnétique en tout point.
Il faut penser au théorème d'Ampère. Faire au préalable une étude des symétries.
Les symétries et invariances donnent :
.
On applique le théorème d'Ampère en prenant un cercle de rayon r qui enlace le fil.
On considère les cas :
:
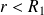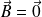(pas de courant enlacé)
Si
:
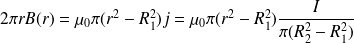
Soit :
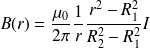
Si
:
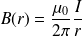
Si
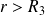: (courant enlacé globalement nul)
Question
Vérifier les relations de passage.
On constate que le champ est bien continu en
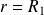et en
(propriété d'une distribution volumique de courants).
En
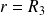: le champ magnétique est discontinu et :
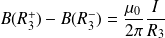
La densité surfacique sur le cylindre de rayon
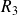est donnée par :
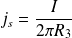
On vérifie bien la relation de passage lors de la traversée d'une surface parcourue par un courant surfacique :
