Théorème d'Ampère
Une vidéo de présentation sur l'électricité et le magnétisme
Rappel :
Le théorème de Stokes, que l'on admet, est le pendant du théorème de Green-Ostrogradsky.
Énoncé du théorème de Stokes :
Soit (C) un contour (c'est-à-dire une courbe fermée orientée) et (S) une surface quelconque qui s'appuie sur (C) (à la manière d'un chapeau dont (C) serait le bord), dont le vecteur normal est orienté selon la règle du tire-bouchon.
Le théorème de Stokes s'écrit :
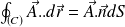
Ce théorème va permettre d'écrire le théorème d'Ampère de manière intégrale, en partant de l'équation de Maxwell-ampère en régime statique :
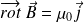
On calcule la circulation à un instant donné du champ magnétique le long d'un contour (C) sur lequel s'appuie une surface (S) et on utilise l'équation de MA :
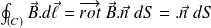
On reconnaît :

L'intensité qui traverse (S).
D'où le théorème d'Ampère :
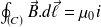
Attention : Flux de B et circulation de B (théorème d'Ampère)
Le champ magnétique est à flux conservatif :
Théorème d'Ampère :
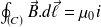
Conseil : Les utilisations classiques du théorème d'Ampère
Le théorème d'Ampère permet de calculer facilement un champ magnétique lorsque les propriétés de symétrie sont fortes, notamment dans les cas classiques suivants qu'il faut connaître :
Fil infini (sans épaisseur) parcouru par un courant I :

On utilise ici la base cylindrique.
Solénoïde de longueur "infinie", comportant n spires par unité de longueur, parcourues par un courant I :

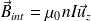
Une animation JAVA de JJ.Rousseau sur le champ d'un solénoïde : cliquer ICI

Champ magnétique créé par un tore (celui de la figure ci-dessus) comportant N spires parcourues par le courant I :

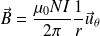

On utilise ici la base cylindrique.
Une animation JAVA de JJ.Rousseau sur le champ d'un tore : cliquer ICI
