Exo 8
Question
Déterminer le réel
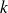 pour que la fonction
pour que la fonction
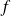 définie sur par :
définie sur par :
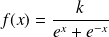 soit une densité de probabilité.
soit une densité de probabilité.
Vérifiez les trois conditions qui définissent une densité.
La fonction
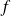 doit vérifier trois conditions :
doit vérifier trois conditions :
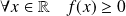 .
.Or :
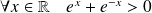 . Donc, il faut que
. Donc, il faut que
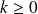 .
.La fonction
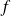 doit être continue sauf en un nombre fini de points.
doit être continue sauf en un nombre fini de points.Or
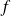 est continue sur
est continue sur
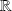 car la fonction exponentielle est continue.
car la fonction exponentielle est continue.L'intégrale
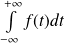 doit être convergente et
doit être convergente et
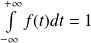 .
.La fonction
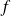 étant paire, il suffit de montrer la convergence de
étant paire, il suffit de montrer la convergence de
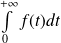 .
.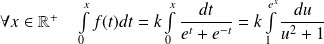 en posant
en posant
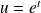 .
.
Donc :
 .
.
Or :
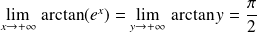 .
.
Donc l'intégrale
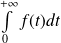 est convergente et
est convergente et
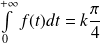 .
.
Donc l'intégrale
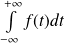 est convergente et
est convergente et
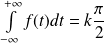 .
.
Conclusion : La fonction
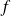 est une densité de probabilité si
est une densité de probabilité si
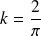 .
.
Question
On définit la variable aléatoire réelle
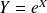 . Déterminer une densité de
. Déterminer une densité de
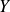 .
.
Commencez par déterminer la fonction de répartition de
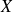 et déduisez celle de
et déduisez celle de
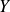 .
.
La fonction de répartition de
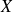 est définie par :
est définie par :
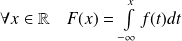 .
.
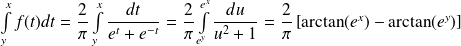 en posant
en posant
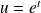 .
.
Or :
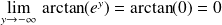 .
.
Donc la fonction de répartition de
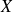 est :
est :
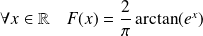 .
.
La fonction de répartition de
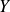 est définie par :
est définie par :
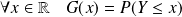 .
.
La variable aléatoire
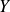 est à valeurs strictement positives.
est à valeurs strictement positives.
Donc
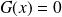 si
si
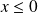 .
.
Si
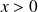 , alors :
, alors :
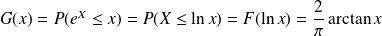 .
.
La fonction
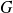 est continue sur
est continue sur
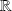 et de classe
et de classe
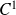 sauf peut-être en
sauf peut-être en
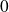 .
.
Pour obtenir une densité de
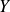 , on dérive sa fonction de répartition sur
, on dérive sa fonction de répartition sur
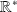 et on complète en
et on complète en
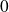 par une valeur arbitraire.
par une valeur arbitraire.
Conclusion : Une densité de
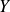 est :
est :
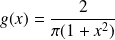 si
si
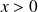 et
et
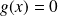 sinon.
sinon.





