Exo 4
Une urne
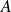contient
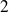boules blanches et
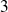boules rouges.
Une urne
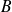contient
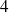boules blanches et
boule rouge.
On effectue une suite de tirages d'une boule avec remise selon le protocole suivant :
On choisit d'abord une des deux urnes au hasard et le premier tirage s'effectue dans cette urne.
Ensuite, à chaque tirage, si la boule tirée est blanche, le tirage suivant est effectué dans la même urne, et sinon, on change d'urne pour effectuer le tirage suivant.
Question
Calculer la probabilité que le
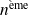tirage ait lieu dans l'urne
.
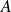Utilisez la formule des probabilités totales.
Soit
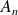l'événement « le
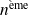tirage a lieu dans l'urne
».
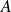Donc :
.
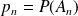Le premier tirage a lieu dans une urne tirée au hasard. Donc :
.
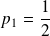Si le
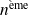tirage a lieu dans l'urne
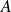, on reste dans l'urne
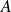si l'on tire une boule blanche et sinon on va dans l'urne
.
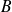Donc :
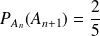et
.
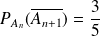Si le
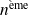tirage a lieu dans l'urne
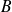, on reste dans l'urne
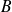si l'on tire une boule blanche et sinon on va dans l'urne
.
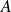Donc :
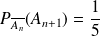et
.
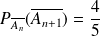D'après la formule des probabilités totales :
.
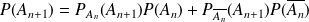Donc :
.
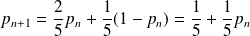La suite
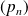est arithmético-géométrique.
Son point fixe vérifie :
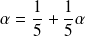. Donc :
.
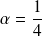Donc la suite
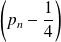est géométrique de raison
.
Donc :
.
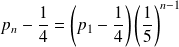Conclusion :
.
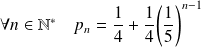Question
Calculer la probabilité que le
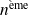tirage donne une boule rouge.
Utilisez la formule des probabilités totales.
Soit
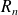l'événement « le
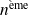tirage donne une boule rouge ».
Donc :
.
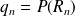D'après la formule des probabilités totales :
.
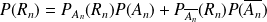Or
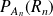est la probabilité de tirer une boule rouge dans
:
.
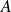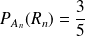Et
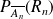est la probabilité de tirer une boule rouge dans
:
.
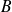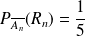Donc :
.
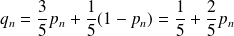Conclusion :
.
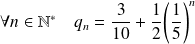