Exo 2
Un sac contient
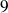boules indiscernables au toucher :
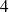boules sont blanches et numérotées de
à
,
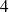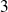boules sont noires et numérotées de
à
,
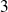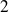boules sont rouges et numérotées
et
.
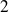On tire simultanément
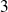boules de ce sac.
Question
Calculer la probabilité de l'événement
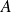: « on obtient plus de boules blanches que de boules noires ».
Effectuez une partition des tirages selon le nombre de boules blanches tirées.
Les boules sont indiscernables au toucher, donc il y a équiprobabilité.
Donc pour tout événement
:
.
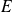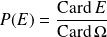On tire simultanément
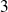boules parmi
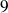. Donc :
.
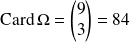L'événement
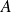est réalisé dans les cas suivants :
on tire trois boules blanches :
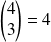.on tire deux boules blanches et une autre (noire ou rouge) :
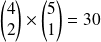.on tire une boule blanche et deux boules rouges :
.
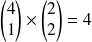Ces événements sont incompatibles.
Donc :
.
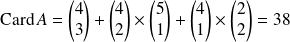Donc :
.
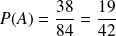Conclusion : La probabilité d'obtenir plus de boules blanches que de boules noires est
.
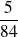Question
Calculer la probabilité de l'événement
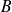: « la somme des numéros est paire ».
Etudiez la parité des numéros pour que leur somme soit paire.
Il y a
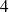numéros pairs et
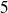numéros impairs (la couleur n'a pas d'importance).
L'événement
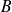est réalisé dans les cas suivants :
les trois numéros sont pairs :
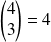
il y a un numéro pair et deux numéros impairs :
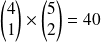
Ces deux événements sont incompatibles.
Donc :
.
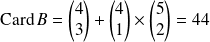Donc :
.
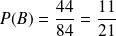Conclusion : La probabilité que la somme des numéros soit paire est
.
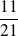