Exo 7
Une urne contient une boule noire et une boule blanche.
On tire une boule de l'urne.
Si elle est noire, le jeu s'arrête.
Si elle est blanche, on la remet dans l'urne et on ajoute une boule blanche.
Et on recommence : on tire une boule de l'urne.
Si elle est noire, le jeu s'arrête.
Si elle est blanche, on la remet dans l'urne et on ajoute une boule blanche.
Et ainsi de suite ....
Soit
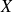le nombre de tirages effectués pour obtenir une boule noire et
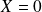si l'on n'en obtient jamais.
Question
Déterminer la loi de probabilité de
.
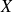Introduisez les événements
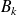l'événement « le
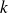-ième tirage donne une boule blanche ».
L'univers image de
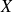est :
.
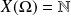Pour tout entier
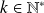, on note
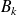l'événement « le
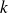-ième tirage donne une boule blanche ».
Le
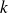-ième tirage a lieu si, auparavant, on n'a tiré que des boules blanches. Alors l'urne contient
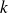boules blanches et une boule noire.
Donc :
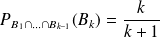et
.
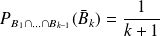Donc :
.
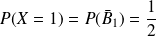Et :
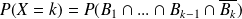si
.
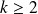D'après la formule des probabilités composées :
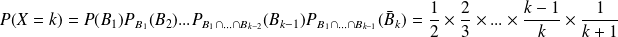
Donc :
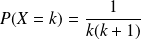si
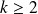. La formule est vraie aussi pour
.
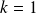Et :
.
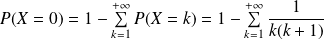Or :
.
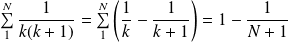Donc :
.
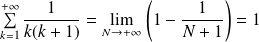Donc :
.
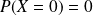Conclusion :
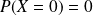et
.
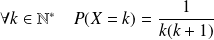Question
La variable aléatoire X a-t-elle une espérance ?
.
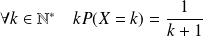C'est le terme général d'une série divergente (Riemann).
Conclusion : La variable aléatoire
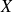n'a pas d'espérance.
