Les trous noirs
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Un trou noir est un corps situé dans l'Univers d'où ni lumière ni matière ne peuvent s'échapper.
L'exercice suivant présente la description classique que pouvait avoir Laplace des trous noirs.
Question
Étoile de Laplace : en 1798, dans « Exposition du système du Monde », Laplace imagine un astre (à répartition de masse sphérique) de même masse volumique moyenne que la Terre (notée
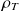) et de rayon égal à 250 fois celui du Soleil.
Quelle est la vitesse de libération
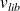correspondante à la surface de l'astre ?
Données :
Distance Terre - Soleil :
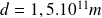
Masse et rayon terrestres :
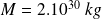et
Constante de la gravitation :
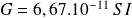
La vitesse de libération
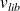est définie comme étant la vitesse minimale (évaluée dans le référentiel « astrocentrique ») à communiquer à un point matériel (de masse m) pour qu'il échappe à l'attraction de l'astre.
Dans ce référentiel (supposé galiléen), l'énergie mécanique du point matériel, soumis uniquement à la force conservative due à l'attraction gravitationnelle de l'astre, se conserve.
A la surface de l'astre, elle vaut (en notant M et R la masse et le rayon de l'astre) :
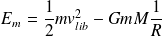
Lorsque le point matériel a échappé à l'attraction de l'astre, son énergie potentielle et sa vitesse sont nulles : son énergie mécanique l'est également, soit :
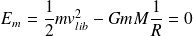
D'où :
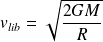
Comme les masses de l'astre et de la Terre peuvent s'écrire
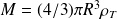et
,
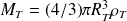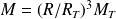et, finalement :
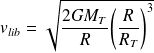
Numériquement :
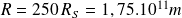et
.
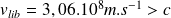Laplace en conclut qu'un tel astre empêche la lumière de quitter la surface de l'astre, le rendant ainsi invisible.
Dans la terminologie actuelle, celle de la relativité générale, un tel « objet » est décrit comme un « trou noir ».
Question
Rayon de Schwarzschild : on admet qu'un corps de masse M agit comme un trou noir si son rayon R est inférieur à un certain rayon critique RC appelé rayon de Schwarzschild, défini par une vitesse de libération à la surface de ce corps égale à la vitesse de la lumière dans le vide, soit
.
Exprimer RC en fonction de G, M et c. Calculer RC dans le cas du Soleil puis de la Terre.
Exprimer la force gravitationnelle
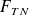exercée par un trou noir sur un objet P en fonction de la masse m de l'objet, de sa distance r au centre du trou noir, du rayon RC du trou noir et de c. Calculer
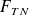pour :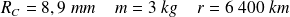 
Calculer l'accélération de la pesanteur
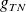au niveau de la sphère de Schwarzschild en fonction de RC et c. Application numérique : calculer
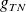pour
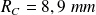.On appelle « sphère des événements » la sphère de rayon RC. Justifier qualitativement le choix de ce terme.
La vitesse de libération étant égale à c pour le rayon de Schwarzschild RC :
soit
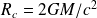
Numériquement :
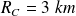pour le Soleil et
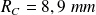pour la Terre.
La force gravitationnelle exercée par le trou noir sur le point P est :
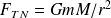
Soit, avec
:
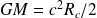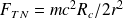
Numériquement :
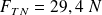
Cette valeur est égale au poids du même objet placé à la surface de la Terre, dont le rayon est justement égal à la distance du point P au centre du trou noir.
L'accélération de la pesanteur à la surface du trou noir vaut :
Soit :
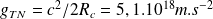
C'est une valeur gigantesque, correspondant au champ créé par un objet de même masse que la Terre mais contenu dans un volume de l'ordre de celui d'une petite bille !
L'intérieur de la sphère de Schwarzschild (de rayon RC) correspond à un volume critique dans lequel la lumière ne peut plus s'échapper.
La lumière reçue par un observateur extérieur ne pourra provenir au mieux que de la surface de la sphère, appelée pour cela « sphère des événements ».
Question
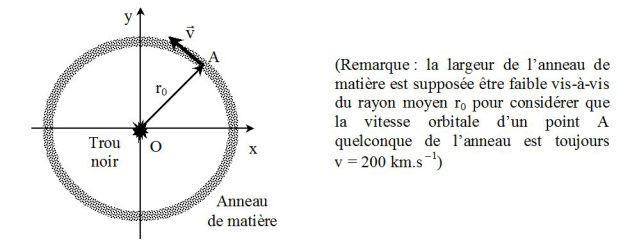
Application au cœur de notre galaxie : des astronomes ont observé un petit objet massif au centre de notre galaxie, autour duquel un anneau de matière est en orbite circulaire.
L'anneau a un diamètre de 15 al (al = année de lumière, distance parcourue par la lumière dans le vide en une année) et sa vitesse orbitale est voisine de
.
En supposant la masse de l'objet massif très supérieure à celle de l'anneau, déterminer la masse
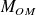de cet objet massif, en kg puis en unité de masse solaire.
La plupart des astronomes pensent actuellement que cet objet massif est un trou noir.
Calculer son rayon de Schwarzschild et comparer la valeur numérique obtenue à la distance moyenne d entre la Terre et le Soleil.
Données :
Distance Terre - Soleil :
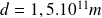
Masse et rayon terrestres :
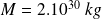et
Constante de la gravitation :
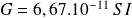
Le référentiel d'étude est celui lié à l'astre massif situé au point O (confondu avec le référentiel barycentrique).
Le principe fondamental de la dynamique appliqué à une particule A de l'anneau de matière (qui possède un mouvement circulaire de rayon r0 et de vitesse v autour du trou noir, voir figure) donne, en projection sur la droite OA :
Soit :
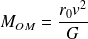
Numériquement, avec
,
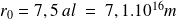, soit plus de 20 millions de fois la masse du Soleil !
Le rayon de Schwarzschild du trou noir est alors
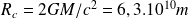, soit 63 millions de km , ce qui correspond à 42% de la distance Terre-Soleil.
De tels trous noirs gigantesques, de masses de l'ordre de plusieurs millions de fois la masse solaire et relativement compacts pourraient être présents à l'intérieur de nombreuses galaxies.
