Vecteur de Runge-Lenz
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On étudie les mouvements dus à une force centrale :
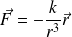
Question
Monter que l'énergie est conservée puis la calculer.
La force découle de l'énergie potentielle :
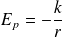
L'énergie mécanique est donc conservée.
Question
Monter que le mouvement est plan.
Le moment de
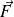est nul donc le moment cinétique est une constante.
Ainsi la vitesse et le mouvement se font orthogonalement à une direction fixe et constante.
Le mouvement est donc plan. On appelle
la direction du moment cinétique :
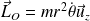
Question
On pose :
Calculer
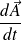puis
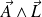. Quelle est la direction de
?
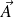Que peut-on dire sur le vecteur
?
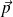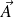est dans le plan du mouvement :
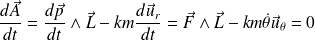
C'est un vecteur constant.
On choisit
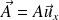. On définit
.
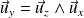On évalue :
On a donc :
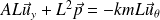
Ainsi,
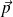parcourt un cercle.
Question
Calculer
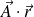. Discuter du mouvement en fonction de la norme de A.
On calcule :
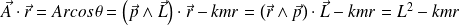
où
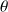est l'angle entre la direction de
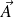et la direction de
.
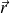On en déduit :
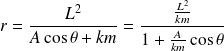
Le mouvement suit donc une conique d'excentricité :
Si
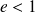: la trajectoire est une ellipse (si
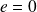, c'est un cercle).Si
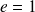: c'est une parabole.Si
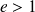: c'est une hyperbole.
