Freinage d'un satellite par l'atmosphère
Consacrer 20 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Un satellite terrestre artificiel (S) de vitesse
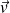(dans le référentiel géocentrique galiléen) sur une orbite basse (c'est-à-dire dont l'altitude z est très inférieure au rayon terrestre RT) subit des frottements dus à l'atmosphère.
Cette force peut se mettre sous la forme :
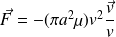
où
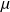est la masse volumique de l'atmosphère et a le rayon du satellite supposé sphérique.
On suppose qu'à l'altitude
:
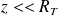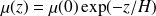
Où
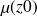et H sont des constantes.
On considère alors que, du fait de la force
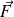, (S) décrit une orbite circulaire autour de la Terre dont le rayon varie lentement avec le temps.
Question
Donner, sous ces hypothèses, une loi approchée de variation de z(t). Il sera avantageux d'introduire la quantité :
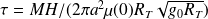
où
désigne le champ de pesanteur terrestre au niveau du sol. On note zi l'altitude de départ.
Retrouver la vitesse et l'énergie mécanique pour une trajectoire circulaire en fonction de l'altitude.
En présence de frottements, la trajectoire reste pratiquement circulaire, au moins sur un tour ...
On suppose que le satellite (S) décrit une orbite circulaire autour de la Terre de rayon r légèrement variable avec le temps.
Par conséquent, la relation entre le rayon r et la vitesse v du satellite ainsi que l'expression de l'énergie mécanique, obtenues pour un satellite circulaire sont encore valables :
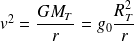
Et :
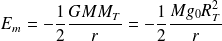
Avec
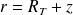et
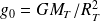(champ de pesanteur terrestre au sol).
La puissance de la force de frottements due aux chocs avec l'atmosphère vaut :
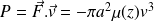
Elle est reliée à la variation de l'énergie mécanique du satellite par
Comme :
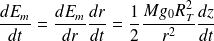
Il vient :
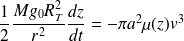
D'où :
Soit, avec :
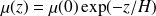
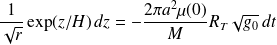
En posant :
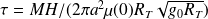
La relation précédente devient :
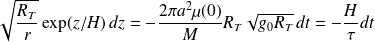
Comme
:
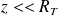Par conséquent :
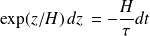
En notant zi l'altitude initiale à l'instant t = 0, l'altitude z atteinte à l'instant t est alors donnée par :
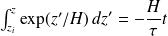
Soit :
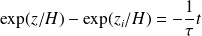
Ou :
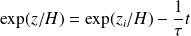
Question
Applications numériques :
Calculer la durée de chute tch du satellite depuis l'altitude
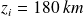jusqu'à
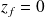. On donne :
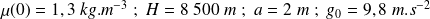
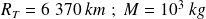
Applications numériques : la durée de la chute vaut :
.
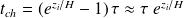Avec
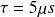, on obtient
.
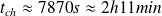La vitesse du satellite reste sensiblement constante lors de la chute (en effet,
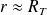et vaut :
