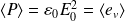Réflexion d'une onde sur un métal "parfait", pression de radiation (calcul ondulatoire)
Consacrer 30 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
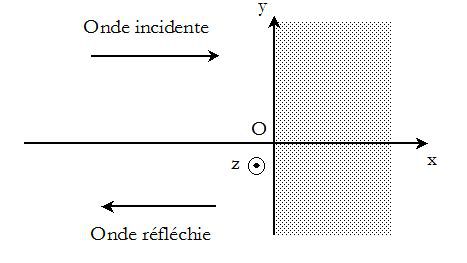
Une OPPM, à polarisation rectiligne, se propage dans le vide dans la direction (Ox), dans le sens des x croissants (on suppose E0 > 0) :
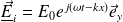
En x = 0, elle arrive sur la surface plane d'un miroir métallique parfaitement conducteur, dans lequel les champs
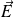et
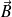sont nuls, et donne naissance à une onde réfléchie se propageant dans le sens des x décroissants :
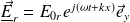
Question
En écrivant les conditions aux limites que doivent vérifier les champs
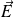et
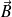en x = 0, déterminer :
L'amplitude E0r du champ réfléchi en fonction de E0.
La charge surfacique
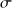et le courant surfacique
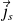qui peuvent se trouver sur la surface métallique en x = 0.
Quelles sont les conditions de passage d'une onde EM à la traversée d'un métal parfait ?
La composante tangentielle du champ électrique doit être continue, par conséquent :
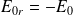
La condition de passage pour le champ électrique :
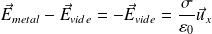
Montre que
.
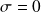La condition de passage pour le champ magnétique donne :
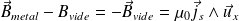
Le champ magnétique incident est :
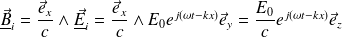
Le champ magnétique réfléchi est :
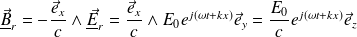
Le champ résultant sur le métal vaut :
On en déduit :
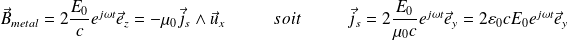
En notation réelle :
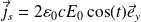
Question
Déterminer le champ électromagnétique résultant de l'onde incidente et de l'onde réfléchie dans le demi-espace x < 0.
Caractériser brièvement l'onde résultante.
Calculer la valeur moyenne de son vecteur de Poynting.
Le champ total est la somme du champ initial et réfléchi.
Qu'est ce qu'une onde stationnaire ?
Le champ électrique résultant est :
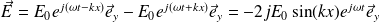
Soit, en notation réelle :
De même, pour le champ magnétique :
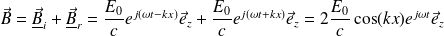
Soit, en notation réelle :
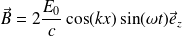
Ce type de solutions, appelé onde plane stationnaire, est très différent d'une onde plane progressive : les dépendances spatiale et temporelle interviennent séparément ; la dépendance spatiale intervient dans l'amplitude de l'oscillation temporelle et non plus dans la phase, de telle sorte que tous les points de la corde vibrent en phase ou en opposition de phase.
En certains points (appelés nœuds de vibrations), le champ est toujours nul.
En d'autres points (appelés ventres de vibrations), l'amplitude de vibration est maximale.
Question
Le champ électromagnétique exerce sur une surface dS du miroir une force
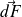dont l'expression est, en notation réelle :
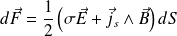
Proposer une explication de la présence du facteur
.
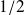En déduire que l'onde exerce une pression P sur le miroir dont on calculera la valeur moyenne <P> en fonction de la densité volumique moyenne d'énergie <ei> de l'onde incidente, puis en fonction de la densité volumique d'énergie totale <etotale> au voisinage immédiat du plan (P est appelée pression de radiation).
Calculer <P> pour une onde incidente fournie par un laser de puissance moyenne <Wi>=3 mW, dont la section droite est s=0,4 mm2.
Le champ électromagnétique exerce sur une surface dS du miroir une force
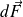dont l'expression est, en notation réelle : (noter que
)
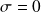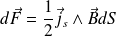
En effet, la surface dS est soumise à l'action du champ magnétique qui lui est extérieur ; il ne faut donc pas prendre en compte le champ magnétique créé par cette surface dS chargée et parcourue par des courants volumiques.
Le facteur 1/2 prend en compte cette remarque.
La valeur moyenne de la force devient :
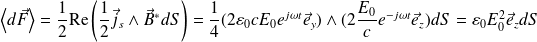
La pression de radiation moyenne est alors :
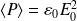
La densité d'énergie volumique est :
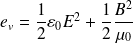
Dont la valeur moyenne est :
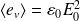
On en déduit :
