Propagation dans un milieu chiral
(20 minutes de préparation)
Un milieu chiral est un milieu transparent dans lequel les ondes circulaires droites et gauches ne se propagent pas à la même vitesse.
Pour les ondes circulaires gauches (resp.droites), l'indice est ng (resp.nd).
On envoie dans un tel milieu une onde initialement polarisée rectiligne selon (Ox) et se propageant dans la direction (Oz).
On supposera qu'à l'interface vide-milieu chiral, la pulsation de l'onde ne varie pas.
On suppose que dans un milieu transparent, le champ EM se propage exactement de la même manière que dans le vide, à la condition de remplacer c par c / n, où n est l'indice du milieu.
Question
Quelle est alors l'équation de propagation du champ électrique dans un milieu d'indice n ? Quelle est la relation entre k et ω pour une onde plane progressive harmonique ?
L'équation de propagation devient :

On a alors :
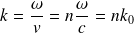
Question
Quelle est l'expression de l'onde dans le milieu chiral ?
On pourra décomposer l'onde incidente en deux ondes polarisées circulairement droite et gauche
On décompose l'onde incidente en deux ondes polarisées circulairement droite et gauche (en notation réelle) :
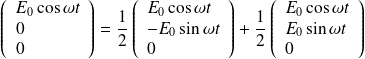
En un point z quelconque, l'onde sera :
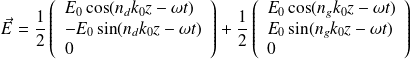
On utilise les formules de trigonométrie :
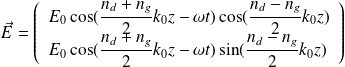
Question
Quelle est, après la traversée d'une cuve de longueur e, la polarisation de l'onde ? Caractériser le changement observé.
On peut ainsi écrire le champ sous la forme :

On constate que le champ a une polarisation rectiligne, selon la direction définie par le vecteur :
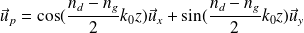
L'angle de rotation à la sortie du milieu est donné par :






