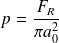Pression de radiation (calcul corpusculaire)
(20 minutes de préparation)
L'énergie E et la quantité de mouvement
d'un photon sont données respectivement par :
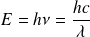et
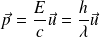
où
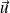est un vecteur unitaire dirigé dans le sens de propagation, h la constante de Planck et c la vitesse de la lumière dans le vide.
On supposera le rayonnement solaire isotrope et monochromatique, de longueur d'onde moyenne λ.
La Terre, située en moyenne à une distance d = 150 millions de km du Soleil, reçoit une puissance de rayonnement solaire par unité de surface égale à
.
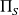On néglige l'absorption du rayonnement solaire par l'atmosphère.
Question
Indiquer comment varie la puissance reçue par unité de surface avec la distance r de la source au récepteur et calculer littéralement la puissance totale P émise par le Soleil sous forme de rayonnement électromagnétique.
Le rayonnement émis par le Soleil étant isotrope, la puissance P émise par le Soleil est également répartie sur une sphère centrée sur le Soleil et de rayon r.
Par conséquent, la puissance reçue par unité de surface à la distance r est :
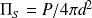
D'où :
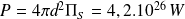
Question
On considère une particule matérielle sphérique, parfaitement réfléchissante, de centre M, de rayon a0 et de masse volumique uniforme
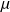, se trouvant à la distance r du Soleil (
).
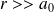La lumière issue du Soleil s'y réfléchit en suivant les lois de l'optique géométrique et l'on supposera que toute la lumière incidente est réfléchie dans la direction arrière comme dans le cas d'un miroir plan sous incidence normale.
Déterminer la valeur moyenne de la force
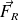due au rayonnement solaire que subit la particule.
On exprimera le résultat littéral en fonction de P, a0 et r.
En déduire la pression exercée par le rayonnement solaire sur la particule.
Un photon, de quantité de mouvement initiale :
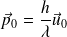
Repart, après réflexion sur la particule M, dans la direction opposée en cédant à celle-ci la quantité de mouvement :
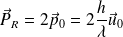
Pendant l'intervalle de temps dt, l'énergie lumineuse dE reçue par la particule :
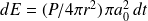
Correspond à un nombre de photons :
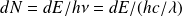
La quantité de mouvement
reçue par la particule pendant dt est alors :
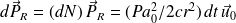
La force moyenne exercée sur la particule est par conséquent :
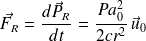
La pression s'en déduit facilement :
