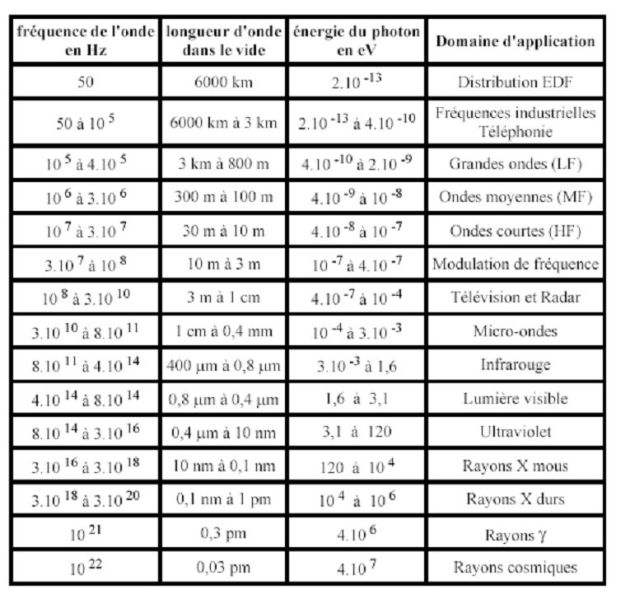
Ondes EM dans le vide
Fondamental : Équation de propagation de d'Alembert
Soit une distribution (D) de charges localisées autour d'un point O, dont les densités sont fonction du temps (exemple : une antenne métallique).
Selon les équations de Maxwell-Gauss et de Maxwell-Ampère, cette distribution (D) est la source de champs
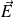 et
et
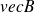 variables dans le temps qui vont s'établir dans tout le voisinage de O.
variables dans le temps qui vont s'établir dans tout le voisinage de O.
Un point M de ce voisinage, bien que situé en dehors de (D), est lui-même source de champs en raison des termes en
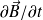 et
et
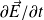 « provenant de O » qui jouent un rôle de sources dans les équations de Maxwell-Faraday et de Maxwell-Ampère.
« provenant de O » qui jouent un rôle de sources dans les équations de Maxwell-Faraday et de Maxwell-Ampère.
Les points P du voisinage de M sont à leur tour dans leur propre voisinage des sources de champs variables dans le temps ...
On conçoit ainsi que le champ EM se propage en faisant penser à des rides se transmettant de proche en proche à la surface de l'eau.
« Le couplage qui est introduit dans les équations de Maxwell par la présence des deux dérivées partielles par rapport au temps
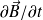 et
et
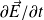 est à l'origine du phénomène de propagation du champ EM. »
est à l'origine du phénomène de propagation du champ EM. »
Obtention des équations de propagation du champ EM :
On calcule le rotationnel de l'équation de Maxwell-Faraday :
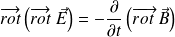
Or :

Avec :

Il vient :
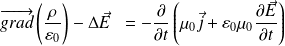
Soit, finalement :
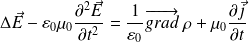
De manière symétrique, on élimine E au profit de B en calculant le rotationnel de MA :
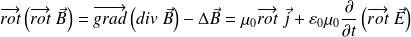
Soit :

Finalement :
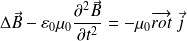
Attention : Équation de propagation de d'Alembert dans le vide
Dans une région sans charges ni courants (
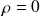 et
et
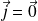 ) :
) :
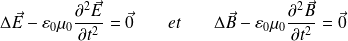
C'est l'équation de d'Alembert (équation classique de propagation des ondes, encore appelée équation des cordes vibrantes) établie au XVIIIème siècle pour modéliser les vibrations d'une corde tendue.
Les solutions de cette équation traduisent un phénomène de propagation de célérité c (vitesse de la lumière dans le vide) :
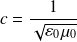
Fondamental : Solution de l'équation de d'Alembert sous forme d'onde progressive
A une dimension, l'équation de d'Alembert s'écrit :
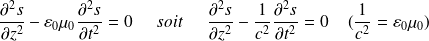
où
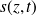 représente une des coordonnées du champ EM, fonction uniquement de
représente une des coordonnées du champ EM, fonction uniquement de
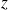 et de
et de
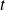 .
.
On démontre qu'une forme de solution de l'équation d'onde de d'Alembert s'écrit sous la forme :
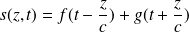
où
 est une fonction quelconque de la variable
est une fonction quelconque de la variable
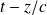 et g une fonction de la variable
et g une fonction de la variable
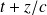 .
.
Interprétation physique :
On considère une fonction de la forme :
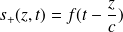
On constate que :
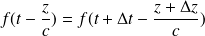
pour tout couple
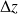 et
et
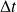 vérifiant :
vérifiant :
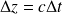
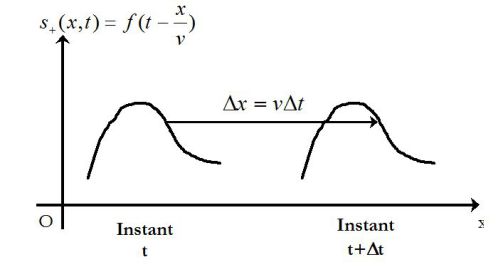
Ainsi,
 représente un signal qui se propage sans déformation à la vitesse c le long de l'axe (Oz) dans le sens positif.
représente un signal qui se propage sans déformation à la vitesse c le long de l'axe (Oz) dans le sens positif.
La solution :
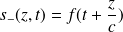
représente un signal qui se propage sans déformation à la vitesse c le long de l'axe (Oz) dans le sens négatif.
Dans un plan
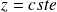 , les fonctions
, les fonctions
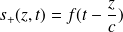 et
et
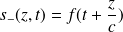 prennent, à tout instant, la même valeur : on parle d'onde plane et les plans
prennent, à tout instant, la même valeur : on parle d'onde plane et les plans
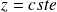 sont appelés des plans d'onde.
sont appelés des plans d'onde.
Une source (par exemple, une station radiophonique) émet a priori des ondes sphériques ; cependant, à grande distance de celle-ci, l'onde reçue pourra être localement assimilée à une onde plane progressive
Ondes planes progressives monochromatiques (ou harmoniques, OPPH) :
L'équation de propagation est linéaire ; par conséquent, l'analyse de Fourier permet d'affirmer que toute solution de cette équation est la somme de fonctions sinusoïdales du temps.
On se limite ici à des solutions harmoniques de l'équation de d'Alembert, c'est-à-dire des solutions de la forme (pour une onde qui se propage dans le sens
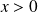 :
:
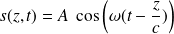
Ces solutions correspondent à des ondes planes progressives harmoniques (OPPH).
Ces fonctions, de période temporelle
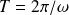 possèdent une période spatiale
possèdent une période spatiale
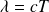 appelée longueur d'onde.
appelée longueur d'onde.
On définit le vecteur d'onde
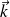 tel que :
tel que :
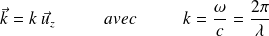
L'OPPH est alors de la forme :
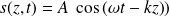
En notation réelle, le champ électrique pourra s'écrire :
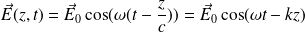
En notation complexe, on notera le champ EM sous la forme :

Si la direction de l'onde est quelconque, dans la direction du vecteur unitaire
 :
:
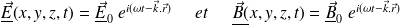
où
 (
(
 vecteur unitaire donnant le sens de propagation) est le vecteur d'onde et
vecteur unitaire donnant le sens de propagation) est le vecteur d'onde et
 (O, origine du repère et M le point d'observation).
(O, origine du repère et M le point d'observation).
Une animation JAVA sur les ondes progressives (JJ.Rousseau, Université du Mans) :
Cliquer ICI
Méthode : Les opérateurs vectoriels pour des OPPH en notation complexe
Compte tenu du choix de la notation complexe, les opérateurs vectoriels se simplifient.
Avec :
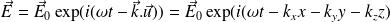
Il vient :
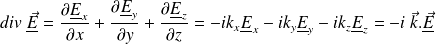
De même :

On peut finalement remarquer que l'opérateur nabla est équivalent à :
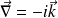
Les quatre équations de Maxwell deviennent ensuite :
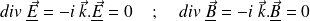
Et :
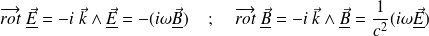
Fondamental : Structure du champ électromagnétique dans le vide
Les équations de Maxwell écrites précédemment donne par exemple :
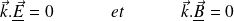
Ainsi, les coordonnées du champ EM parallèles à la direction de propagation sont nulles : le champ EM est transversal.
On obtient également, à partir de l'équation de Maxwell-Faraday :

Finalement, les champ EM d'une onde plane progressive sont orthogonaux à la direction de propagation et orthogonaux entre eux.
Le trièdre
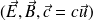 est direct et
est direct et
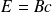 .
.
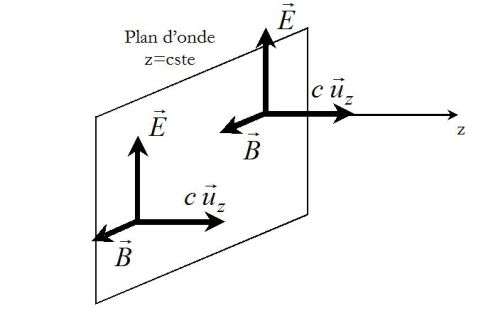
Remarques importantes :
La relation de structure d'une onde plane :

n'est vérifiée évidemment que par des ondes planes monochromatiques harmoniques.
Notamment, lorsque l'amplitude de l'onde dépendra des coordonnées d'espace x ou y, la relation entre le champ
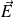 et le champ
et le champ
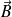 sera différente.
sera différente.Force de Lorentz :
La force exercée par l'onde EM sur une particule de charge q et de vitesse
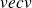 est :
est :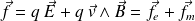
Par conséquent, le rapport de la force électrique sur la force magnétique vaut :
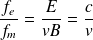
Par conséquent, pour une particule non relativiste (
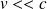 ), la force magnétique est négligeable vis-à-vis de la force électrique.
), la force magnétique est négligeable vis-à-vis de la force électrique.
Complément : Une vidéo de cours sur les radiocommunications
Fondamental : Propagation de l'énergie
Les résultats qui suivent sont valables pour une onde plane progressive, non forcément sinusoïdale (ou harmonique).
La densité d'énergie
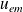 pour une onde plane progressive vaut :
pour une onde plane progressive vaut :
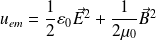
Compte tenu de
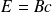 , il vient (et avec
, il vient (et avec
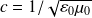 ) :
) :

On remarque qu'il y a équipartition des contributions électrique et magnétique à cette densité d'énergie.
Le vecteur de Poynting vaut :
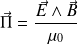
Soit, avec
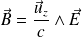 :
:
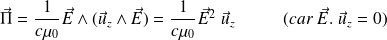
Finalement :
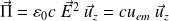
Le vecteur de Poynting est bien colinéaire à la direction de propagation ; si l'on revient à la définition du vecteur densité de courant :

correspondant à un mouvement d'ensemble de charges de densité
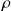 à la vitesse
à la vitesse
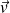 , on constate que la relation
, on constate que la relation
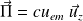 exprime simplement que l'onde EM plane progressive dans le vide transporte l'énergie dans sa propre direction de propagation et avec une vitesse égale à sa célérité
exprime simplement que l'onde EM plane progressive dans le vide transporte l'énergie dans sa propre direction de propagation et avec une vitesse égale à sa célérité
 (
(
 ).
).
Remarque (vitesse de propagation de l'énergie) :
On peut retrouver ce résultat en considérant le cylindre de section droite (S) et de génératrices de longueur
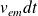 parallèles à la direction de propagation.
parallèles à la direction de propagation.
L'énergie qui va traverser cette surface pendant dt est alors
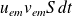 .
.
Elle est par ailleurs égale au flux du vecteur de Poynting (multiplié par dt), soit :
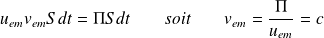
Vecteur de Poynting moyen et puissance moyenne reçue par un détecteur :
Les ondes EM ont généralement des fréquences élevées.
Les détecteurs ne sont souvent sensibles qu'aux valeurs moyennes temporelles de la puissance qu'ils reçoivent.
Ainsi, la puissance moyenne reçue par un détecteur dont la surface S est perpendiculaire à la direction de propagation est :

où
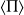 désigne la valeur algébrique du vecteur de Poynting moyen, égale à :
désigne la valeur algébrique du vecteur de Poynting moyen, égale à :
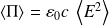
Pour un champ électrique de la forme :
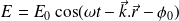
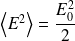
Et ainsi :
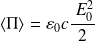
Utilisation de la notation complexe pour la puissance :
Si
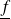 et
et
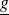 sont deux fonctions sinusoïdales en notation complexe, alors la partie réelle moyenne du produit fg est :
sont deux fonctions sinusoïdales en notation complexe, alors la partie réelle moyenne du produit fg est :

où
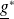 est le conjugué de
est le conjugué de
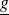 .
.
On peut notamment appliquer cette formule pour calculer la puissance moyenne en électricité :

La valeur moyenne de la densité d'énergie EM est alors :

Soit :
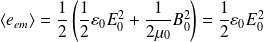
La valeur moyenne du vecteur de Poynting se calcule de la même manière :
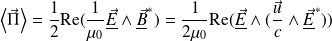
Soit :

Quelques ordres de grandeur :
Amplitudes des champs EM d'un faisceau laser :
Un laser hélium-néon émet un faisceau cylindrique de section droite
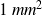 et de puissance 1 mW.
et de puissance 1 mW. Il produit une onde polarisée rectilignement.
Déterminer l'amplitude des champs EM.
L'onde est quasi-plane sinusoïdale car la largeur du faisceau est bien supérieure à la longueur d'onde.
Les champs EM valent :

Émission d'une station radio :
Une source d'onde EM monochromatique (E) située dans une plaine émet un rayonnement isotrope polarisé rectilignement de puissance 1 MW.
Calculer l'amplitude du champ électrique à la distance r puis à 1 000 km.
On trouve :

Complément : Solution de l'équation de d'Alembert sous forme d'onde stationnaire
On cherche des solutions de l'équation de d'Alembert de la forme (méthode de séparation des variables) :

En substituant dans l'équation de d'Alembert :
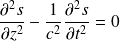
Il vient :
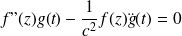
D'où :

On obtient ainsi deux équations différentielles :

Ou encore :
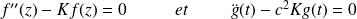
Si
 , la solution de la deuxième équation différentielle est de la forme :
, la solution de la deuxième équation différentielle est de la forme :
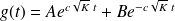
Cette solution est à rejeter : en effet, elle correspond soit à une solution divergente soit à une solution transitoire.
Dans la suite, on suppose
 ; alors, en posant
; alors, en posant
 :
:
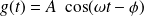
La 1ère équation donne alors :

La solution globale de l'équation de d'Alembert est alors :
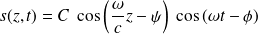
On pose dans la suite
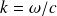 , alors :
, alors :
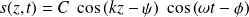
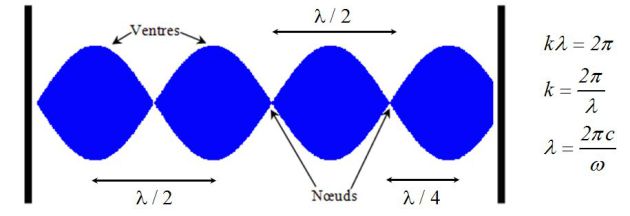
Ce type de solutions, appelé onde plane stationnaire est très différent d'une onde plane progressive : les dépendances spatiale et temporelle interviennent séparément ; la dépendance spatiale intervient dans l'amplitude de l'oscillation temporelle et non plus dans la phase, de telle sorte que tous les points de la corde vibrent en phase ou en opposition de phase.
L'allure de la corde à différents instants est représentée sur la figure suivante.
Certains points de la corde sont fixes et sont appelés nœuds de vibrations ; d'autres ont une amplitude de vibration maximale et sont appelés ventres de vibrations.
La distance entre deux nœuds successifs est égale à
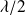 .
.
La distance entre deux ventres successifs est égale à
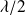 .
.
La distance entre un nœud et un ventre successif est égale à
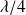 .
.
Une animation JAVA sur les ondes stationnaires de JJ.Rousseau (Université du Mans) :
Cliquer ICI