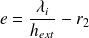Isolation d'une conduite de vapeur
(15 minutes de préparation)
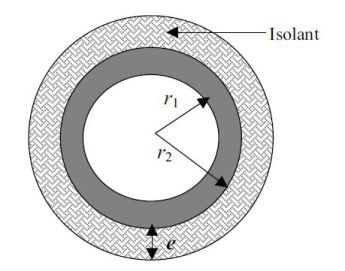
On considère une conduite cylindrique en acier de rayon interne
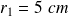et de rayon externe
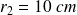et de longueur
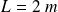. On note
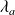la conductivité thermique de l'acier.
Elle canalise une vapeur surchauffée de température
.
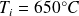L'air extérieur est à la température
.
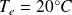On isole cette canalisation à l'aide d'un isolant d'épaisseur
, de forme cylindrique et de conductivité thermique
.
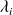Question
Déterminer les résistances thermiques de conduction de la conduite en acier et de l'isolant.
On considère un cylindre d'acier de rayon
, de même axe que la conduite de vapeur.
En régime stationnaire, le flux
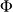à travers la surface latérale de ce cylindre est constant :
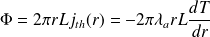
Ainsi :
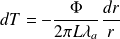
En intégrant de
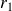à
:
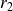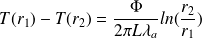
On en déduit la résistance thermique de l'acier :
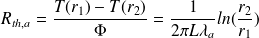
De même, la résistance thermique de l'isolant est :
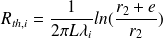
Question
On note
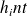le coefficient de convection entre la vapeur d'eau et l'acier et
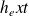le coefficient de convection entre l'isolant et l'air extérieur.
En utilisant la loi de Newton, déterminer les résistances de convection de la conduite ainsi isolée.
Le flux thermique de convection entre l'eau et l'acier vaut (orienté vers l'extérieur de la conduite) :
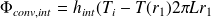
Par conséquent, la résistance thermique de convection est :
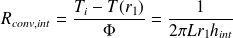
De même, la résistance thermique de convection entre l'isolant et l'air extérieur est :
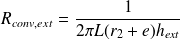
Question
Déterminer la résistance thermique équivalente, notée
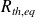, de la conduite ainsi isolée.
Les différentes résistances thermiques, parcourues par le même flux thermique, sont placées en série.
Par conséquent, la résistance totale équivalente vaut la somme des résistances thermiques calculées dans les questions précédentes :
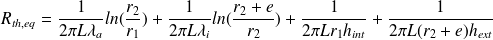
Question
Justifier, qualitativement puis quantitativement, l'existence d'une épaisseur optimale pour laquelle la résistance équivalente
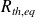est maximale.
On constate que la couche d'isolant augmente la résistance de conduction mais diminue la résistance de convection.
Pour déterminer l'épaisseur optimale, on peut évaluer :
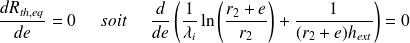
On peut poser la variable intermédiaire :
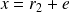
Alors :
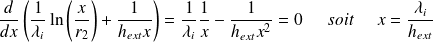
On en déduit l'épaisseur optimale d'isolant :
