Mesure expérimentale d'une conductivité thermique
(15 minutes de préparation)
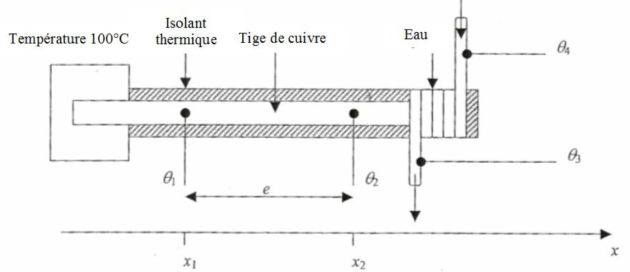
On réalise le montage suivant afin de mesurer la conductivité thermique K du cuivre.
L'extrémité gauche de la barre cylindrique de cuivre, de section S = 11,5 cm2, est placée dans une étuve maintenue à 100°C.
L'autre extrémité est en contact avec un serpentin dans lequel circule de l'eau (de capacité thermique massique c = 4,18 kJ.K-1.kg-1) avec un débit massique Dm = 0,80 g.s-1. L'échangeur thermique ainsi constitué permet de réchauffer l'eau de θ4 à θ3.
La barre est calorifugée latéralement à l'aide d'enveloppes isolantes.
On mesure les températures θ1 à θ2 de la barre en deux points de celle - ci distants de e = 10 cm ainsi que les températures θ4 à θ3 de l'eau juste avant et après la zone d'échange thermique.
Le problème est unidimensionnel, le matériau homogène et on négligera tout phénomène de rayonnement et de convection au niveau de la barre.
Question
Pourquoi calorifuge-t-on la surface latérale de la barre ? Citer un exemple de matériau isolant thermique pouvant être utilisé dans ce montage ?
Matériau isolant : mousse de polystyrène ou laine de verre.
Question
On attend que le régime stationnaire soit établi. En appliquant l'équation de la conduction thermique, exprimer la température T(x) le long de la barre en fonction de la variable x et des constantes x1, e, T1 et T2.
L'équation de la conduction thermique est :
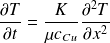
Question
Déterminer la puissance thermique traversant la section S de la barre. Celle - ci dépend-elle de x ?
En régime stationnaire :
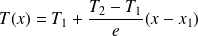
La puissance thermique est :
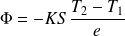
Question
Déterminer la puissance thermique reçue par l'eau circulant dans le serpentin en fonction de θ4 à θ3 (on pourra d'abord réaliser un bilan sur la masse dm d'eau traversant le serpentin pendant dt).
Le 1er principe de la thermodynamique donne :
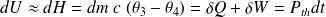
D'où :
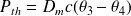
Question
En déduire l'expression de la conductivité thermique K du cuivre.
On obtient expérimentalement K = 374. Donner l'unité de K.
L'échangeur est parfait :
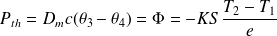
D'où :