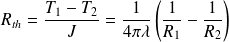Résistance thermique
(10 minutes de préparation)
On considère deux sphères concentriques S1 et S2, de rayons R1 et R2, qui sont portées aux températures T1 et T2.
L'espace entre les deux sphères est un milieu de conductivité thermique k.
Question
Calculer, en régime permanent, la puissance calorifique J (flux thermique) passant de S1 vers S2.
Montrer que le rapport (T1-T2)/J est une constante Rth (résistance thermique).
On effectue un bilan d'énergie entre les instants t et t + dt, en prenant comme volume élémentaire le volume compris entre les deux sphères de rayons r et r + dr (soit 4πr2dr) :
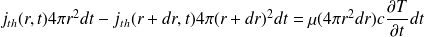
Soit :

On se place en régime stationnaire :
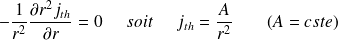
Le flux thermique J est donné par :
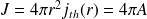
D'où :
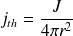
La loi de Fourier donne :
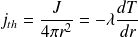
D'où, en intégrant entre les deux sphères :
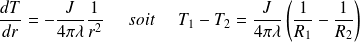
D'où l'expression de la résistance thermique :