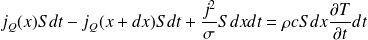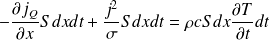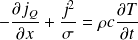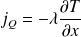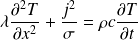Conductions thermique et électrique
(10 minutes de préparation)
On considère un milieu conducteur de la chaleur et de l'électricité (de conductivité thermique λ, de chaleur massique c, de masse volumique ρ et de conductivité électrique
).
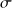Le milieu, infini dans les directions (Oy) et (Oz), est limité par les plans x = 0 et x = L :
En x = 0 : on a un thermostat de température T0.
En x = L, on a placé une paroi adiabatique.
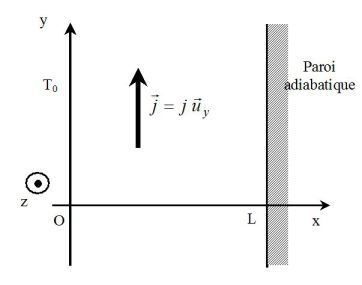
Le milieu est parcouru par un courant électrique dont la densité volumique de courant est uniforme :
Les seuls transfert de chaleur considérés ici sont de nature conductive.
Question
La température entre les deux plans x = 0 et x = L est a priori une fonction de x, y , z et du temps t.
Montrer que T ne dépend que de x et du temps, T(x,t).
Déterminer, en régime quelconque, l'équation aux dérivées partielles vérifiée par T(x,t), appelée équation de la chaleur.
Démontrer l'équation de la chaleur en présence de sources. La puissance électrique est ici (volumique)
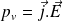, avec
.
Invariances par translation selon Oy et Oz : T(x,t) uniquement.
Un bilan d'énergie réalisé sur un volume élémentaire donne : (figure de gauche ci - dessous)
Soit :
D'où :
Avec : (loi de Fourier)
On obtient l'équation de la chaleur avec sources :
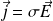Question
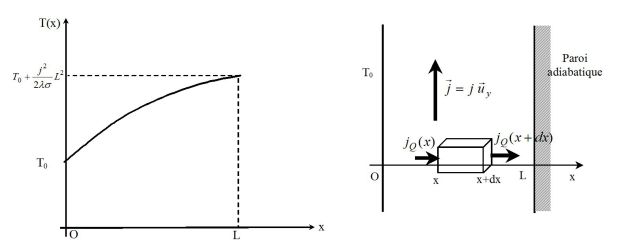
Calculer la température T(x) en régime stationnaire en un point M compris entre les plans x = 0 et x = L.
Tracer la courbe T(x). En quel point la température est-elle extrémale ?
En régime stationnaire :
Conditions aux limites :
En x = 0, T = T0, donc b = T0.
En x = L, la paroi est adiabatique, par conséquent le vecteur densité de courant d'énergie y est nul :
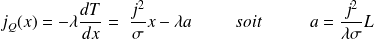
Finalement :
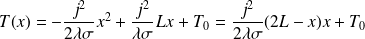
La température est maximale lorsque jQ est nul (soit x = L) et vaut :
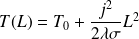
La courbe représentant T(x) est donnée ci - dessus.
