Résistances thermiques
Rappel : Résistances thermiques
Définition de la résistance thermique d'une tige cylindrique isolée :
On souhaite déterminer, en régime permanent, la température dans une tige homogène cylindrique de section S, de longueur L et dont les extrémités sont maintenues aux températures T1 et T2 < T1.
On suppose que la surface latérale est isolée.
L'équation de la chaleur devient simplement :
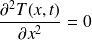
Soit :
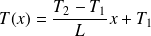
Le flux thermique qui traverse la tige est :
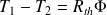
Soit :
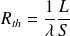
On définit également la conductance thermique :
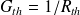
Attention : Définition de la résistance thermique
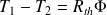
Exemple : Isolation des murs d'une maison
Parpaings, polystyrène, placoplâtre et papier-peints : résistances thermiques en série
Idem mais avec une fenêtre en plus : résistances thermiques en parallèle
Prenons le cas d'un double vitrage associant une vitre de surface S, d'épaisseur e / 3 et de conductivité λ, une épaisseur de gaz peu dense de conductivité λ' et une deuxième vitre identique à la première.
Il s'agit de l'association en série de trois résistances thermiques, d'où la résistance thermique de l'ensemble :
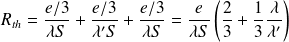
où le premier terme e/λS est la résistance thermique d'une vitre simple de même encombrement. Avec λ'=λ/100, on voit que le double vitrage permet de multiplier la résistance thermique par 102/3=34 et donc de diviser par 34 les pertes à travers la vitre.
Complément : Analogie entre les lois phénoménologiques de Fourier et d'Ohm
Le modèle classique de Drude permet d'interpréter la loi d'Ohm locale dans les métaux :
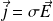
On rappelle l'expression de la résistance électrique R d'un fil métallique de longueur L, de section transverse S et de conductivité sigma (de résistivité ρ) :
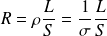
On fait évidemment l'analogie avec la résistance thermique d'un barreau rectiligne unidimensionnel.
