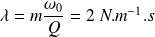Portrait de phase d'un oscillateur
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
On considère le portrait de phase d'un oscillateur harmonique amorti composé d'une masse
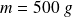, soumise à une force de rappel élastique (ressort de raideur k) et à une force de frottement fluide (
) ,
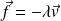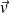étant la vitesse de la masse m.
On note x l'écart à la position d'équilibre).
L'étude est réalisée dans le référentiel galiléen du laboratoire.
Question
Déterminer la nature du régime de l'oscillateur.
Régime pseudo-périodique : présence de frottements, la courbe de phase n'est pas fermée.
Elle se termine en un point d'équilibre stable (ici le point O), appelé attracteur.
Question
Déterminer, par lecture graphique :
La valeur initiale de la position
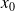.La valeur finale de la position
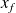.La pseudo - période
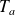.Le décrément logarithmique
.
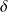Par lecture directe du diagramme :
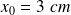et
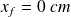
De même, la pseudo-période vaut :
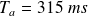
Le décrément logarithmique est :
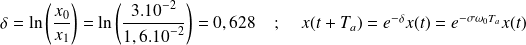
Question
En déduire la pulsation propre
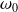, le facteur de qualité Q de l'oscillateur, la raideur k du ressort et le coefficient de frottement fluide
.
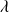On trouve :
,
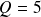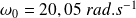et
On note que
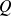donne l'ordre de grandeur du nombre d'oscillations visibles.
On en déduit :
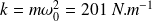et
