Gravitation et troisième loi de Kepler
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
Notre galaxie, dont la trace sur le ciel nocturne est appelée « voie lactée », est un système formé d'un grand nombre d'étoiles animées autour de leur centre de masse commun de mouvements orbitaux supposés analogues à ceux des planètes autour du Soleil.
La figure suivante représente le schéma de notre galaxie vue en coupe avec ses trois caractéristiques : bulbe central, disque et halo sphérique d'amas d'étoiles (appelé amas globulaires).
Le Soleil est localisé au niveau du disque galactique, à une distance D = 30 000 al du cœur de la galaxie ; il décrit autour du noyau galactique une orbite circulaire en une période TS = 250.106 années.
On supposera que toutes les masses confinées à l'intérieur d'une sphère de rayon D agissent comme si elles se trouvaient au centre de la galaxie.
Question
Donner une estimation grossière de la masse M de la galaxie, en kg puis en unité de masse solaire.
Données :
Redémontrer la 3ème loi de Kepler.
En supposant que toutes les masses confinées à l'intérieur de la sphère de rayon D agissent comme si elles se trouvaient au centre de la galaxie (et en négligeant les masses extérieures à la sphère de rayon D), la 3ème loi de Kepler peut s'appliquer au mouvement circulaire du Soleil autour du cœur de la galaxie. Par conséquent :
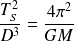
Soit :
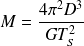
Numériquement :
,
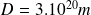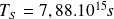, d'où
.
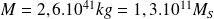Soit une masse de la voie lactée évaluée à 130 milliards de fois celle du Soleil.
Question
Comparer le nombre M/MS à l'évaluation N = 6.1011 déduite par les astronomes à partir d'études de rotation de notre galaxie.
Interpréter simplement l'écart entre ces deux valeurs.
Données :
Le rapport
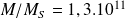évalué en supposant la masse de la galaxie essentiellement répartie dans le bulbe central est inférieur à l'évaluation
effectuée à partir de calculs plus sophistiqués.
L'écart entre ces deux valeurs s'explique en notant que le halo sphérique comporte un grand nombre d'étoiles dont les masses ne sont pas prises en compte lors de l'évaluation simpliste réalisée à la question précédente.
