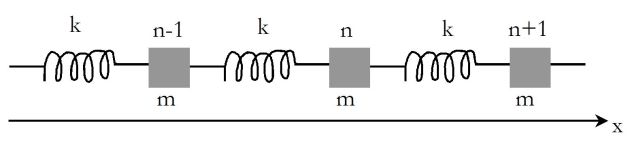
Dispersion sur une chaîne d'atomes
(15 minutes de préparation)
On veut montrer qu'il existe des ondes élastiques longitudinales de pulsation
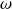et de vecteur d'onde
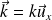pouvant se propager le long d'un e chaîne infinie d'atomes, de masse m, de constante de raideur K et de positions au repos
.
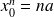En notation complexe, le déplacement de la masse numérotée n est :
Question
Pourquoi A ne dépend-il pas de n ?
L'onde n'est ni stationnaire ni amortie : tous les atomes ont donc même amplitude pour une onde progressive. Le système est globalement invariant par translation.
Ainsi, A ne dépend pas de l'atome considéré.
Question
Déterminer, en fonction de
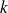, les valeurs possibles de la pulsation
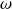des ondes susceptibles de se propager sur la chaîne.
Que déduit-on de la non linéarité de cette relation ?
Le PFD appliqué à l'atome numéroté n donne :
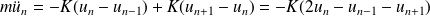
On injecte la solution proposée dans cette équation :
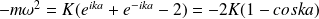
Soit :
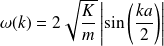
Cette relation de dispersion est non linéaire : il y a dispersion.
Question
Calculer les vitesses de phase
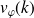et de groupe
.
Donner leurs limites pour
et
et les commenter.
La vitesse de phase est : (on se place dans la suite dans le cas où
)
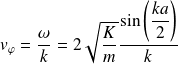
Et la vitesse de groupe :
Pour
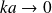(donc des grandes longueurs d'onde) :
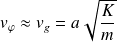
On retrouve les vitesses obtenues dans l'approximation des milieux continus.
Et pour
:
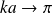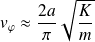
Et :
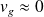
L'onde ne passe plus.
