Un modèle de propagation du son dans l'air
Consacrer 15 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
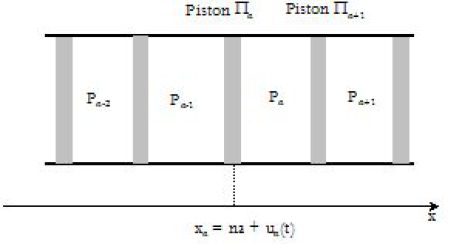
Un tuyau calorifugé de section S est partagé en une infinité de compartiments (Cn) par des pistons calorifugés Pn et Pn+1 de section S et de masse m.
Dans chaque compartiment se trouve une mole d'air, assimilé à un GP évoluant de manière isentropique selon la loi de Laplace
.
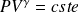A l'équilibre, l'abscisse du piston (n) vaut :
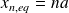
et la pression a la même valeur P0 dans chaque compartiment.
Hors équilibre, l'abscisse du piston (n) vaut :
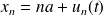
avec
et la pression dans le compartiment (n) vaut Pn.
Question
Établir l'expression de la pression Pn en fonction de P0, g, a, un et un+1 et la linéariser en utilisant
.
En déduire l'équation différentielle linéaire déterminant le mouvement du piston numéro (n).
La loi de Laplace est-elle vérifiée ?
N'oubliez pas que
.
L'application de la loi de Laplace pour le gaz dans le compartiment n conduit à :
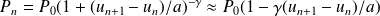
Question
On fait l'approximation des milieux continus en définissant une fonction u(x,t) variant peu à l'échelle de a, telle que
.
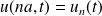Établir l'équation aux dérivées partielles dont est solution u(x,t).
Définir une célérité c et commenter son expression.
Le PFD appliqué au piston numéro n donne :
L'approximation des milieux continus aboutit à :
D'où :
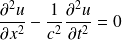
Avec :
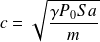
c augmente si le milieu est plus rigide (P0 augmente) et moins inerte (m diminue), ce qui est naturel pour des ondes mécaniques.
Question
Évaluer la célérité c du son dans l'air en supposant que les pistons de masse m du modèle sont en réalité constitués par le volume d'air V = Sa compris entre deux pistons dans le modèle.
On donne :
(masse volumique de l'air dans les CNTP)
AN :
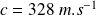(en bon accord avec la valeur attendue)
