Ondes sonores sphériques
(15 minutes de préparation)
Une sphère pulsante de centre fixe O dont le rayon :
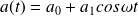
varie sinusoïdalement avec une amplitude
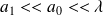, émet des ondes sonores dans tout l'espace extérieur à la sphère, rempli d'air de masse volumique
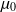où la vitesse des ondes sonores vaut
.
Compte tenu de la symétrie du problème, on cherche en coordonnées sphériques de centre O un champ de pression de la forme :
et on rappelle que, pour un champ scalaire
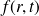, le laplacien peut s'écrire :
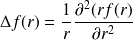
Question
1) Déterminer la forme générale des solutions
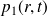de l'équation de d'Alembert et interpréter.Justifier qu'on doit choisir :
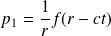
Question
2) Dans la suite, on pose
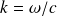et on cherche une solution de la forme :
Déterminer le champ des vitesses correspondant.
Comment se simplifie l'expression de
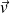pour
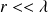? En déduire les expressions de
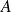et de
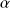.En déduire la puissance moyenne rayonnée à travers une sphère de rayon
.
Question
On définit une solution stationnaire :
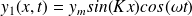
Montrer que les conditions aux limites permettent d'exprimer une condition sur
.
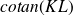