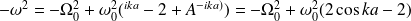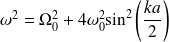Équation de propagation de Klein-Gordon
Consacrer 10 minutes de préparation à cet exercice.
Puis, si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Si vous avez des questions complémentaires, n'hésitez pas à les poser sur le forum.
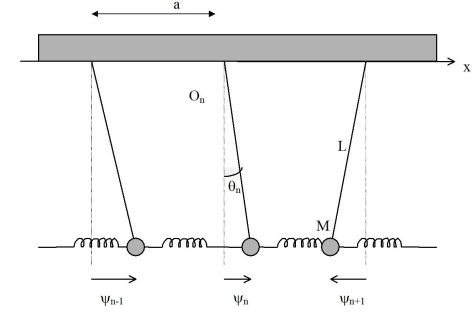
On étudie la propagation d'onde le long d'une chaîne de pendules simples, identiques, de masse M et de longueur L, couplés par des ressorts de constante K, représentés sur la figure ci-dessous :
On notera :
et
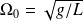
Question
Quelle est l'équation de propagation liant les petits déplacements
,
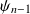et
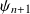des extrémités des pendules ?
Utiliser le théorème du moment cinétique pour chaque pendule par rapport au point d'attache
.
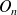Le théorème du moment cinétique appliqué au pendule (n) donne :
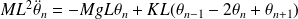
D'où l'équation de propagation :
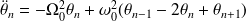
Question
Question
Représenter la relation de dispersion en précisant la bande permise pour les pulsations d'oscillations libres de la chaîne de pendules couplés.
L'intervalle de pulsations possible est (zone de Brillouin) :
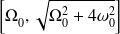
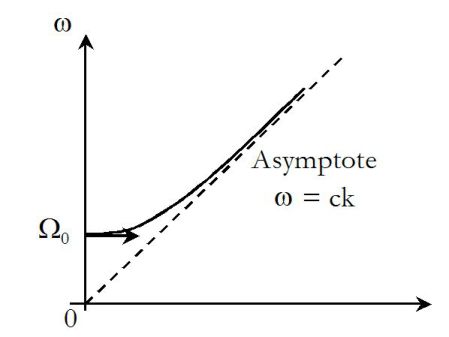
On peut tracer ω en fonction de k (figure ci - dessous).
Question
Préciser la forme prise par ces résultats dans l'approximation des milieux continus.
Dans l'approximation des milieux continus :
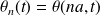
Alors :
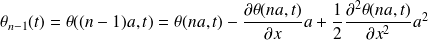
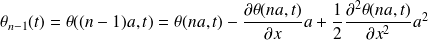
En reportant dans l'équation de propagation :
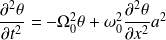
Finalement :
C'est l'équation de Klein-Gordon.
La relation de dispersion prend alors la forme :
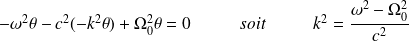
Simulation : Animations JAVA de JJ.Rousseau (Université du Mans)
Pendules couplés par un ressort : cliquer ICI
