Isolation phonique
(15 minutes de préparation)
Pour étudier l'atténuation sonore introduite par un mur, on adopte le modèle sommaire suivant :
Dans un tuyau de section S, une onde sonore incidente plane progressive harmonique de pulsation ω arrive sur un piston de surface S, d'épaisseur e et de masse volumique
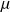 , libre de se déplacer au voisinage de x = 0.
, libre de se déplacer au voisinage de x = 0.
On note c la vitesse du son dans l'air et
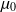 la masse volumique de l'air.
la masse volumique de l'air.
On cherche un champ des vitesses de la forme :
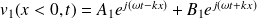
Et :
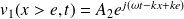
Question
Justifier ces expressions et écrire les surpressions
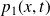 correspondantes.
correspondantes.
Le piston créé une onde réfléchie :
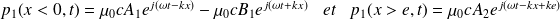
Question
Écrire les conditions aux limites sur le piston indéformable et en déduire que :
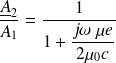
La continuité des vitesses donne :
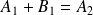
Le théorème du CI appliqué au piston donne (la vitesse du piston est par exemple donnée par
 ) :
) :
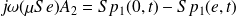
Soit :

On en déduit alors :
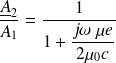
Question
En déduire le facteur de transmission en puissance T du mur.
On donne :
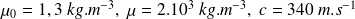
Quelle doit être l'épaisseur minimale du mur si on veut une atténuation d'au moins - 40 décibels pour
 puis pour
puis pour
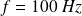 ?
?
Le facteur de transmission en puissance T du mur est ici :
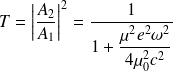
On souhaite une atténuation de – 40 dB (au moins). Par conséquent,
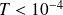 .
.
On obtient
 à
à
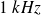 et
et
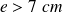 à
à
 .
.





