Référentiel barycentrique
Rappel :
Le mouvement du système est étudié dans le référentiel (R).
On note G le centre d'inertie du système.
On appelle référentiel barycentrique (Rb) relatif au référentiel (R), le référentiel de centre G et animé d'un mouvement de translation à la vitesse
 par rapport à (R).
par rapport à (R).
La loi de composition des vitesses s'écrit sous la forme :
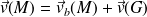
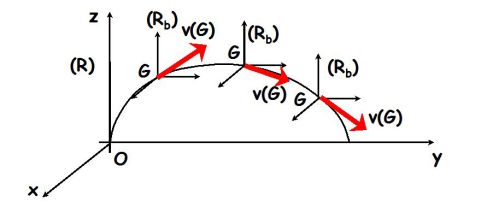
La figure précédente schématise le mouvement d'un ballon de rugby sans frottement dans le champ de pesanteur terrestre :
Le centre d'inertie G du ballon suit une trajectoire parabolique dans le référentiel terrestre galiléen.
Dans le référentiel barycentrique, le ballon tourne autour d'un axe fixe passant par G.
Remarque : Référentiel galiléen ?
Le référentiel barycentrique n'est pas nécessairement galiléen !
Il ne sera galiléen que si le référentiel de centre G et animé d'un mouvement de translation rectiligne uniforme.
Fondamental : Les théorèmes de Koënig
On considère un système (discret ou continu) de centre d'inertie G.
Le référentiel d'étude galiléen est noté (R), d'origine O.
(Rb) désigne le référentiel barycentrique.
Théorème de Koënig pour le moment cinétique :
"Le moment cinétique par rapport à O du système est égal au moment cinétique barycentrique augmenté du moment cinétique du point G affecté de la masse totale m du système par rapport à O."
Pour un solide, de moment d'inertie par rapport à son axe de rotation
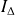 :
: 
Théorème de Koënig pour l'énergie cinétique :
"L'énergie cinétique du système est égale à l'énergie cinétique évaluée dans le référentiel barycentrique augmentée de celle du centre d'inertie G affecté de la masse totale m du système."
Pour un solide :
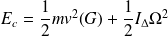
Simulation : Une animation JAVA de JJ.Rousseau (Université du Mans)
Mouvement du centre de masse : cliquer ICI





