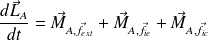Théorème du moment cinétique pour un solide en rotation autour d'un axe fixe
Fondamental : Théorème du moment cinétique en un point fixe
On considère un point fixe A du référentiel galiléen (R).
Alors :
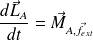
La dérivée du moment cinétique du système par rapport au point fixe A est égal au seul moment en A des forces extérieures au système (celui des forces intérieures est nul).
Fondamental : Théorème du moment cinétique par rapport à un axe fixe
On considère un axe
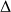passant par A, de vecteur unitaire
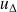, fixe dans (R).
En projetant le théorème du moment cinétique sur cet axe, on obtient le théorème du moment cinétique par rapport l'axe
:
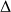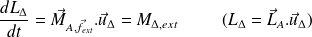
En utilisant :
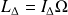
où
désigne la vitesse angulaire du solide, portée par l'axe
.
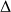Finalement (théorème « scalaire » du moment cinétique pour un solide en rotation autour de l'axe de rotation
) :
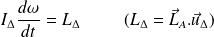
Exemple : Une vidéo d'Alain Le Rille
Exemple : La boite qui remonte les pentes
Fondamental : Lois de la dynamique dans un référentiel non galiléen
Il faut prendre en compte les forces d'inertie :
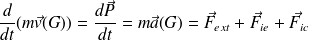
Et, en un point fixe du référentiel mobile :
