Pendule pesant et pendule de torsion
Fondamental : Étude du pendule pesant
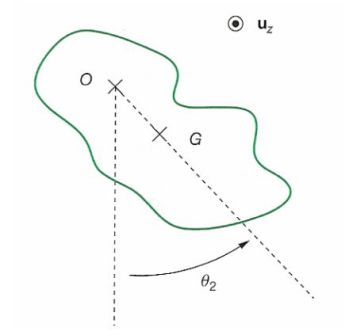
On considère le pendule pesant de la figure suivante.
On note
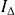 le moment d'inertie de ce pendule par rapport à l'axe de rotation
le moment d'inertie de ce pendule par rapport à l'axe de rotation
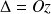 .
.
La liaison pivot en O est supposée parfaite.
On note
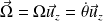 le vecteur vitesse angulaire du pendule,
le vecteur vitesse angulaire du pendule,
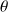 étant l'angle avec la verticale (voir figure).
étant l'angle avec la verticale (voir figure).
Application du théorème du moment cinétique :
Le moment cinétique du pendule par rapport à l'axe de rotation
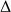 est :
est :
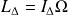
Le moment du poids par rapport à O est :
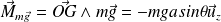
où
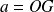 .
.
La réaction du support, appliquée en O, a un moment nul.
Par conséquent, le théorème du moment cinétique par rapport à l'axe de rotation donne directement :
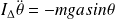
Étude énergétique :
La liaison étant parfaite, la réaction du support ne travaille pas.
Le pendule pesant est un système conservatif. Son énergie mécanique est :

En dérivant par rapport au temps, on retrouve l'équation différentielle précédente.
Cas des petits mouvements :
On peut alors assimiler
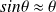 . Ainsi :
. Ainsi :
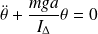
C'est l'équation différentielle d'un oscillateur harmonique de pulsation :
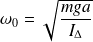
Remarque : dans le cas d'un pendule simple, il suffit d'écrire que
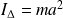 .
.
Complément : Une vidéo de Walter Lewin : "Gravity, pendulums and conservation of energy"
Fondamental : Étude du pendule de torsion
Un pendule de torsion est un dispositif constitué d'une barre horizontale, fixée à un support par l'intermédiaire d'un fil de torsion.
Ce fil d'acier exerce un couple de rappel, proportionnel à l'angle de torsion
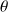 qu'on lui impose :
qu'on lui impose :
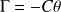
où
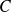 est la constante de torsion du fil.
est la constante de torsion du fil.
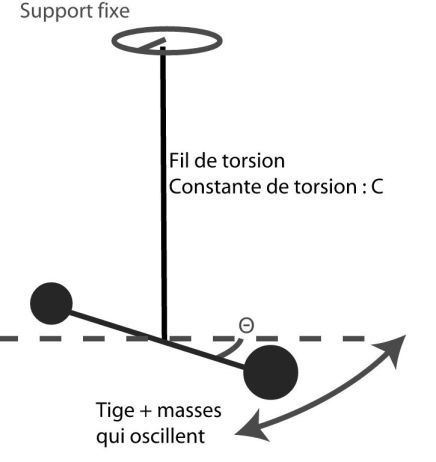
Étude mécanique :
Le théorème du moment cinétique donne, en l'absence de frottements :
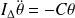
On obtient un oscillateur harmonique de pulsation :
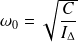

Étude énergétique :
La puissance du couple de torsion est :
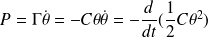
On peut ainsi définir l'énergie potentielle de torsion du fil :
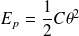
qui est l'analogue de l'énergie potentielle d'un oscillateur harmonique en translation,
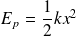 , où
, où
 représente l'élongation du ressort par exemple.
représente l'élongation du ressort par exemple.
Simulation : Animations Java (par JJ.Rousseau, Université du Mans)
Période d'un pendule simple : cliquer ICI
Pendule à longueur variable : cliquer ICI
Pendules couplés par un ressort : cliquer ICI
Pendule de torsion : cliquer ICI
Constante de torsion d'un fil : cliquer ICI
Pendule de torsion double : cliquer ICI
Pendules de torsion couplés : cliquer ICI
Pendule cycloïdal ou pendule de Huygens : cliquer ICI
Pendule accéléré : cliquer ICI
Pendule de Holweck-Legay : cliquer ICI
Pendule elliptique : cliquer ICI





