Étude énergétique d'un solide en rotation
Rappel : Étude énergétique du système de deux points matériels
Dans le cas d'un système de deux points matériels, le travail des forces intérieures peut s'écrire :
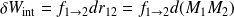
Ce travail, a priori, n'est pas nul sauf dans le cas de deux points matériels rigidement liés l'un à l'autre (
).
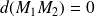Ce travail des forces intérieures sera ainsi nul pour un solide.
Fondamental : Puissance des actions exercées sur un solide
En faisant appel à la notion de forces volumiques
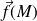exercées sur un solide, on peut écrire la puissance des actions (extérieures et intérieures) exercées sur un corps continu :
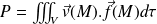
En écrivant que pour un solide (formule de Varignon) :
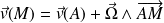
Il vient (A est un point quelconque du solide) :
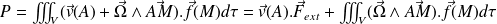
En utilisant (permutation circulaire dans le produit mixte) :
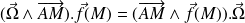
Il vient :
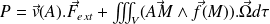
Soit, finalement :
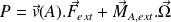
On remarque que les forces intérieures n'interviennent pas dans cette expression de la puissance reçue par le solide.
Remarque :
A pourra être souvent le centre d'inertie G.
Fondamental : Théorème de l'énergie cinétique (ou de la puissance cinétique)
Dans la suite, on se place dans un référentiel (R) supposé galiléen.
Pour un solide :
Ainsi (Théorème de la puissance cinétique) :
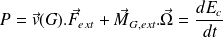
Rappelons ici que P représente la puissance uniquement des actions extérieures subies par le solide (la puissance des actions intérieures est nulle pour un solide).
Le théorème de l'énergie cinétique s'en déduit :
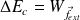
Fondamental : Énergie potentielle et énergie mécanique d'un système
L'énergie mécanique
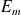d'un système (S) est la somme de son énergie cinétique
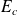et de l'énergie potentielle intérieure
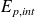et extérieure
:
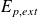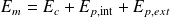
et le théorème de l'énergie cinétique conduit, pour un système fermé (S) à :
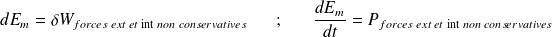
La plupart des actions mécaniques connues sont conservatives (le poids, la force électrique, la force de gravitation, l'action d'un ressort, ...).
Parmi les actions mécaniques non conservatives, on peut citer les actions de contact entre solides, la tension d'un fil, les forces de pression, les forces de propulsion, ...
Conservation de l'énergie mécanique d'un système fermé, système conservatif :
Si toutes les actions mécaniques dérivent d'une énergie potentielle (extérieure ou intérieure) ou si toutes les actions mécaniques qui ne dérivent par d'une énergie potentielle ne travaillent pas, alors l'énergie mécanique du système se conserve au cours du mouvement.
Le système est dit conservatif.
L'équation :
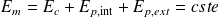
est appelée l'intégrale 1ère du mouvement (relative à l'énergie).
Fondamental : Puissance des actions mécaniques de contact
On a vu que la puissance des actions exercées sur un solide est :
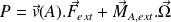
où A est un point quelconque du solide.
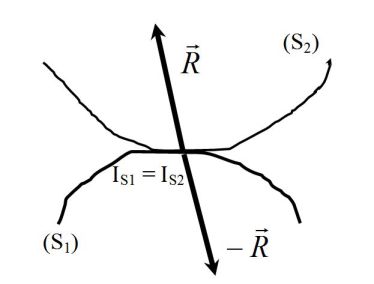
On s'intéresse à l'action du solide (S1) sur le solide (S2).
Le contact est supposé ponctuel en I.
On note
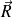la résultante de l'action de (S1) sur le solide (S2).
Alors, la puissance reçue par le solide (S2) de la part du solide (S1) est (le moment est nul puisque le contact est ponctuel) :
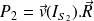
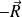désigne la résultante de l'action de (S2) sur le solide (S1).
Alors, la puissance reçue par le solide (S1) de la part du solide (S2) est :
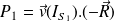
La puissance totale des actions de contact entre les deux solides est alors :
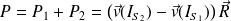
Soit, avec :
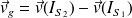
la vitesse de glissement de (S2) par rapport à (S1) :
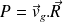
Soit encore, puisque la composante
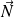est perpendiculaire à la vitesse de glissement :
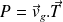
Conséquences des lois de Coulomb :
Il y a glissement :
Alors,
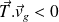et
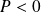. A cause des frottements entre les solides, leur énergie mécanique totale diminue.
Il y a roulement sans glissement :
Alors la vitesse de glissement est nulle et
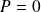. Les actions de contact ne dissipent aucune énergie alors qu'il existe la plupart du temps une composante tangentielle non nulle de frottement.
Très souvent, le solide (S1) est le sol immobile ; alors :
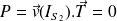
En cas de roulement sans glissement, la puissance des actions de contact du sol immobile sur un solide est nulle.
Application à la résolution des problèmes :
L'étude d'un mouvement avec contact de solides fait intervenir notamment les forces de contact comme inconnues.
Pour résoudre le problème, il faut écrire :
Les équations découlant du principe fondamental des systèmes.
Une relation supplémentaire provenant d'une hypothèse sur l'existence ou non d'un glissement, hypothèse qui devra être vérifiée.
Si l'on suppose qu'il y a glissement, la relation supplémentaire est alors donnée par la loi de Coulomb :
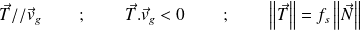
Il faut ensuite vérifier que la vitesse de glissement est bien non nulle et de sens opposé à
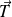.Si l'on suppose qu'il n'y a pas glissement, la relation supplémentaire est
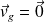et il faut alors vérifier que
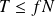.Enfin, si le mouvement comporte différentes phases successives de natures différentes (avec et sans glissement), la vérification de l'hypothèse choisie permet de déterminer l'instant de changement de phase.
