Moment d'inertie d'un solide
Fondamental : Définition du moment d'inertie d'un solide par rapport à un axe
On considère un solide (S) en rotation autour d'un axe
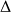lié au solide et fixe dans (R) (Oxyz).
Très souvent, le référentiel d'étude sera le référentiel barycentrique (Rb) (Gxyz) et les axes (Oz) et (Gz) seront soient confondus soient parallèles à l'axe de rotation
.
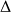Le solide est supposé homogène et on notera :
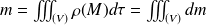
la masse totale du système.
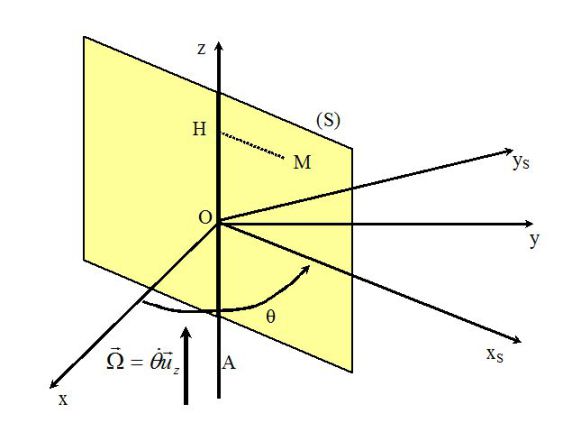
On prend l'exemple d'un solide symétrique par rapport à l'axe de rotation (Oz).
Le solide tourne à la vitesse angulaire
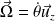autour de l'axe (Oz).
On veut calculer le moment cinétique du solide dans le référentiel (R) par rapport à un point A quelconque situé sur l'axe de rotation :
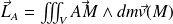
Or :
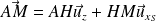
Et le vecteur vitesse est :
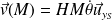
Soit (et on note dans la suite
) :
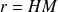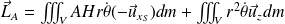
La première intégrale s'annule par symétrie par rapport à l'axe de rotation (considérer le point M' symétrique de M par rapport à Oz : la distance AH est la même mais les vecteurs unitaires
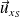sont opposés).
Ainsi :
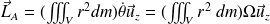
On définit
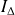le moment d'inertie du solide par rapport à l'axe de rotation
:
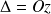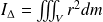
Le moment cinétique du solide autour de l'axe (ou en un point quelconque de l'axe) est :
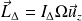
où
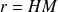désigne la distance du point M à l'axe de rotation.
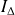est une caractéristique du solide et ne dépend que de la répartition des masses dans le solide.
Exemple : Exemples de moment d"inertie
Tige de longueur 2b, axe passant par son centre :
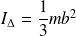
Cerceau de rayon R, axe passant par son centre :
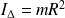
Disque ou cylindre plein de rayon R, axe passant par son axe :
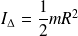
Sphère creuse de rayon R, axe passant par un diamètre :
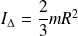
Sphère pleine de rayon R, axe passant par un diamètre :
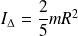
Fondamental : Énergie cinétique de rotation
L'énergie cinétique du système dans (R) est :
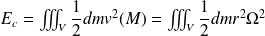
Soit :
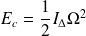
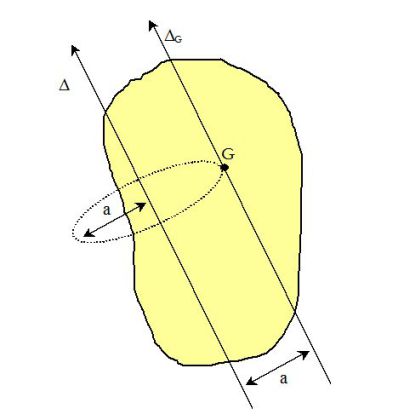
Complément : Le théorème de Huygens
Le théorème de Huygens permet de relier les moments d'inertie
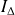d'un solide par rapport à un axe
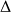et
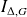du solide par rapport à l'axe
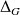parallèle à
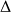et passant par G :
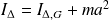
où a désigne la distance entre les deux axes de rotation.
L'énergie cinétique du solide dans (R) est :
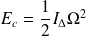
G a (dans le référentiel (R)) un mouvement circulaire de rayon a et de vitesse angulaire
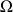, par conséquent :
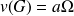
Le théorème de Kœnig relatif à l'énergie donne alors :
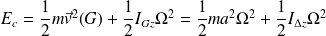
D'où :
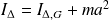
Exemple : Énergie cinétique d'une roue qui roule sans glisser sur un sol horizontal
On peut calculer l'énergie cinétique d'une roue (qui roule sans glisser) dans le référentiel du sol.
Dans le référentiel barycentrique :
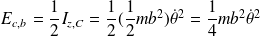
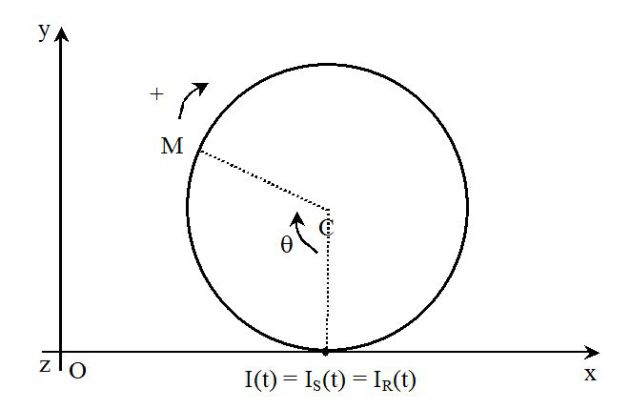
Le théorème de Kœnig relatif à l'énergie donne :
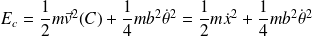
Si on suppose que la roue roule sans glisser :
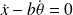
D'où :
