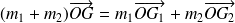Centre d'inertie d'un système
Rappel :
Distribution discontinue :
On étudie un ensemble de
points, notés
, de masse
.
Le centre d'inertie de l'ensemble de ces points est le barycentre des points
affectés des coefficients
.
Par conséquent :
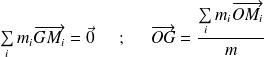
Distribution continue volumique (pour un solide) :
Les formules sont similaires, il suffit juste de remplacer les sommes discrètes par des intégrales :
Ou encore :
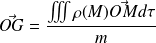
où
est la masse volumique du solide et
sa masse totale.
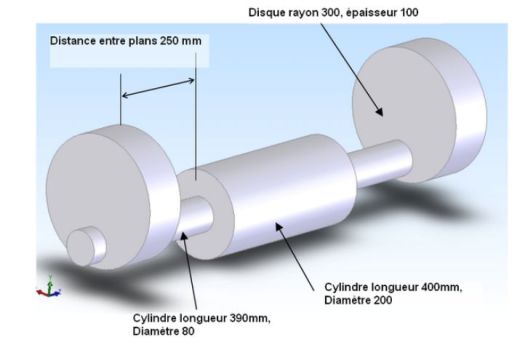
Quel est le centre d'inertie de ce solide ?
Le centre d'inertie possède la propriété d'associativité :
Le centre d'inertie G d'un système (S), constitué de deux systèmes S1 et S2 de masse m1 et m2 et de centres d'inertie G1 et G2, est défini par :
