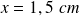Les référentiels non galiléens
Exemple : Le champ de pesanteur terrestre
La force de pesanteur terrestre qui agit sur un corps est la résultante de la force de gravitation universelle exercée par la Terre sur ce corps et de la force d'inertie centrifuge due à la rotation propre de la Terre.
Si l'on assimile le globe terrestre à une sphère de centre O, de rayon
 et de répartition de masse à symétrie sphérique, alors le champ de pesanteur à la surface de la Terre s'écrit, en norme :
et de répartition de masse à symétrie sphérique, alors le champ de pesanteur à la surface de la Terre s'écrit, en norme :
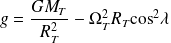
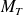 désigne la masse de la Terre,
désigne la masse de la Terre,
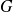 la constante de gravitation universelle,
la constante de gravitation universelle,
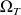 la vitesse angulaire de rotation de la Terre autour de son axe Nord-Sud et
la vitesse angulaire de rotation de la Terre autour de son axe Nord-Sud et
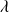 la latitude du point M où l'on calcule
la latitude du point M où l'on calcule
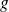 (voir figure).
(voir figure).
La direction du vecteur champ de pesanteur au point M définit la verticale du lieu.
Remarque :
Sur la figure, l'importance de la composante centrifuge, par rapport à l'attraction universelle, a été considérablement exagérée pour plus de clarté.
En effet, le terme
 vaut, au maximum :
vaut, au maximum :
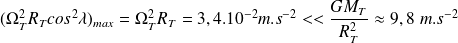
On a noté, sur la figure :
O : Paris
Ox : dirigé vers l'Est et tangent au parallèle du lieu.
Oy : dirigé vers le Nord et tangent au méridien du lieu.
Oz : dirigé selon le rayon terrestre CO et dirigé vers l'extérieur de la Terre.
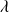 est la latitude du lieu.
est la latitude du lieu.
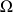 est la vitesse angulaire de la Terre autour de l'axe NS :
est la vitesse angulaire de la Terre autour de l'axe NS :

Remarque :
Du fait de sa rotation propre, la Terre se déforme ; elle n'est plus sphérique mais est aplatie aux pôles.
On définit alors l'ellipsoïde de référence qui est la forme théorique du globe terrestre qui épouse le plus parfaitement possible la forme réelle de la Terre.
Cet ellipsoïde est défini par :
Son rayon équatorial, noté a :

Son aplatissement, noté
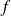 , défini par :
, défini par :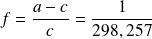
où
 est le rayon polaire.
est le rayon polaire.
Le rayon polaire
 est de l'ordre de
est de l'ordre de
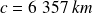 , ce qui correspond à une différence de 21 km entre le rayon polaire et le rayon équatorial (soit une différence relative de 0,3%).
, ce qui correspond à une différence de 21 km entre le rayon polaire et le rayon équatorial (soit une différence relative de 0,3%).
La forme mathématique qui se rapproche au mieux de la forme de la Terre n'est pas une sphère mais n'en est pas très éloignée.
Exemple :
Une vidéo sur les effets de la force centrifuge
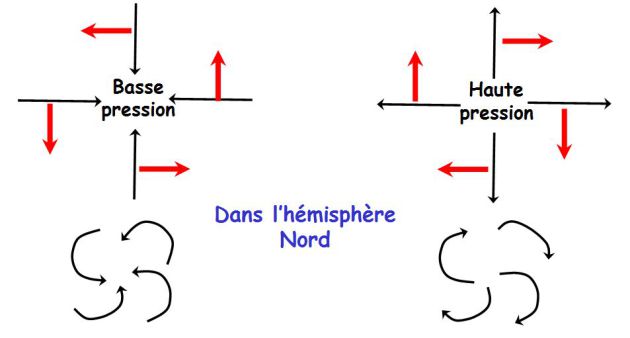
Exemple : Effet de la force de Coriolis : enroulements des dépressions et des anticyclones
Pour des déplacements parallèles au sol :
Un mobile se déplace selon un méridien ou un parallèle.
La force de Coriolis est toujours dirigée vers la droite dans le sens du mouvement (dans l'hémisphère Nord) et vers la gauche dans le sens du mouvement (dans l'hémisphère Sud).
On le montre à partir de la définition de la force de Coriolis :
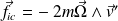
Dans l'hémisphère Nord :
La rive droite des fleuves est souvent plus érodée que la rive gauche
Les rails de chemin de fer sont davantage usés à droite.
Enroulements des dépressions et des anticyclones :
La figure suivante explique de manière qualitative le sens des enroulements des dépressions et des anticyclones dans l'hémisphère nord (c'est le contraire dans l'hémisphère sud).
Exemple : Effet de la force de Coriolis : déviation vers l'Est
On prend le cas d'une chute libre verticale : (les notations sont celles définies sur la première figure)
Un mobile se trouve à l'instant t = 0 sur l'axe (Oz) à une hauteur h.
On le lâche sans vitesse initiale (pas de frottements).
Dans l'hypothèse où le référentiel terrestre est galiléen, la chute libre est verticale et on peut écrire :
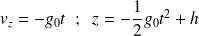
La prise en compte de la force de Coriolis entraîne une légère déviation vers l'Est (force dirigée selon les x > 0) :
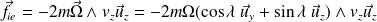
Soit :
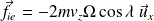
En remplaçant la vitesse selon l'axe (Oz) par son expression obtenue quand le référentiel terrestre est supposé galiléen, on obtient un ordre de grandeur de la force de Coriolis :
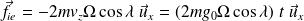
Le temps de chute
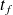 se calcule également en supposant la chute verticale, soit :
se calcule également en supposant la chute verticale, soit :
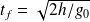
L'ordre de grandeur de la déviation observée est, avec
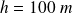 et
et
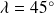 :
: